Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yamamuro, Sadayuki
1985.
Absolute values in orthogonally decomposable spaces.
Bulletin of the Australian Mathematical Society,
Vol. 31,
Issue. 2,
p.
215.
Yamamuro, Sadayuki
1986.
Symmetry groups on ordered Banach spaces.
Bulletin of the Australian Mathematical Society,
Vol. 33,
Issue. 2,
p.
177.
Dang, T.B
and
Yamamuro, S
1986.
On homomorphisms of an orthogonally decomposable Hilbert space.
Journal of Functional Analysis,
Vol. 68,
Issue. 3,
p.
366.
Iochum, B.
1990.
Positive maps on self-dual cones.
Proceedings of the American Mathematical Society,
Vol. 110,
Issue. 3,
p.
755.


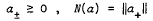 and
and 