Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Aigner, M.
Erd�s, P.
and
Grieser, D.
1987.
On the representing number of intersecting families.
Archiv der Mathematik,
Vol. 49,
Issue. 2,
p.
114.
Füredi, Zoltán
1988.
Matchings and covers in hypergraphs.
Graphs and Combinatorics,
Vol. 4,
Issue. 1,
p.
115.
Frankl, Peter
Ota, Katsuhiro
and
Tokushige, Norihide
1995.
Uniform intersecting families with covering number four.
Journal of Combinatorial Theory, Series A,
Vol. 71,
Issue. 1,
p.
127.
Lemons, Nathan
and
Palmer, Cory
2008.
The Unbalance of Set Systems.
Graphs and Combinatorics,
Vol. 24,
Issue. 4,
p.
361.
CHIBA, Shuya
FURUYA, Michitaka
MATSUBARA, Ryota
and
TAKATOU, Masanori
2012.
Covers in 4-uniform Intersecting Families with Covering Number Three.
Tokyo Journal of Mathematics,
Vol. 35,
Issue. 1,
Frankl, Peter
and
Tokushige, Norihide
2016.
Invitation to intersection problems for finite sets.
Journal of Combinatorial Theory, Series A,
Vol. 144,
Issue. ,
p.
157.
Frankl, Peter
2018.
Resilient Hypergraphs with Fixed Matching Number.
Combinatorica,
Vol. 38,
Issue. 5,
p.
1079.
Cao, Mengyu
Lv, Benjian
and
Wang, Kaishun
2021.
The structure of large non-trivial t-intersecting families of finite sets.
European Journal of Combinatorics,
Vol. 97,
Issue. ,
p.
103373.
Balogh, Jozsef
Lemons, Nathan
and
Palmer, Cory
2021.
Maximum Size Intersecting Families of Bounded Minimum Positive Co-degree.
SIAM Journal on Discrete Mathematics,
Vol. 35,
Issue. 3,
p.
1525.
Liu, Xizhi
and
Mubayi, Dhruv
2021.
Tight bounds for Katona’s shadow intersection theorem.
European Journal of Combinatorics,
Vol. 97,
Issue. ,
p.
103391.
Nagy, Dániel T.
and
Patkós, Balázs
2022.
Triangles in intersecting families.
Mathematika,
Vol. 68,
Issue. 4,
p.
1073.
Frankl, Peter
and
Kupavskii, Andrey
2023.
Uniform intersecting families with large covering number.
European Journal of Combinatorics,
Vol. 113,
Issue. ,
p.
103747.
Füredi, Zoltán
Jiang, Tao
Kostochka, Alexandr
Mubayi, Dhruv
and
Verstraëte, Jacques
2023.
Extremal Problems for Hypergraph Blowups of Trees.
SIAM Journal on Discrete Mathematics,
Vol. 37,
Issue. 4,
p.
2397.
Zhang, Menglong
and
Feng, Tao
2023.
The structure of maximal non-trivial d-wise intersecting uniform families with large sizes.
Discrete Mathematics,
Vol. 346,
Issue. 10,
p.
113533.
Kupavskii, Andrey
and
Zakharov, Dmitrii
2024.
Spread approximations for forbidden intersections problems.
Advances in Mathematics,
Vol. 445,
Issue. ,
p.
109653.
Huang, Yang
and
Peng, Yuejian
2024.
Stability of intersecting families.
European Journal of Combinatorics,
Vol. 115,
Issue. ,
p.
103774.
Magnan, Van
Palmer, Cory
and
Wood, Ryan
2024.
A generalization of diversity for intersecting families.
European Journal of Combinatorics,
Vol. 122,
Issue. ,
p.
104041.
Frankl, Peter
and
Wang, Jian
2025.
Intersecting families with covering number three.
Journal of Combinatorial Theory, Series B,
Vol. 171,
Issue. ,
p.
96.
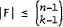 and that if equality holds then τ(F) = 1. Hilton and Milner determined max|F| for τ(F) = 2. In this paper we solve the problem for τ(F) = 3.
and that if equality holds then τ(F) = 1. Hilton and Milner determined max|F| for τ(F) = 2. In this paper we solve the problem for τ(F) = 3.