Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T04:55:10.476Z Has data issue: false hasContentIssue false
  • English
  • Français

ON INTEGRAL ESTIMATES OF NONNEGATIVE POSITIVE DEFINITE FUNCTIONS

Part of: Inequalities Harmonic analysis in one variable

Published online by Cambridge University Press:  13 March 2017

ANDREY EFIMOV ,
MARCELL GAÁL  and
SZILÁRD GY. RÉVÉSZ
ANDREY EFIMOV
Affiliation:
Ural Federal University, 620000 Ekaterinburg, pr. Lenina 51, Russia email [email protected]
MARCELL GAÁL*
Affiliation:
Bolyai Institute, University of Szeged, 6720 Szeged, Aradi vértanúk tere 1, Hungary MTA-DE ‘Lendület’ Functional Analysis Research Group, Institute of Mathematics, University of Debrecen, 4010 Debrecen, PO Box 12, Hungary email [email protected]
SZILÁRD GY. RÉVÉSZ
Affiliation:
Institute of Mathematics, Faculty of Sciences, University of Pécs, 7622 Pécs, Vasvári Pál u. 4, Hungary A. Rényi Institute of Mathematics, Hungarian Academy of Sciences, 1053 Budapest, Reáltanoda u. 13-15, Hungary email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 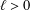$\ell >0$ be arbitrary. We introduce the extremal quantities

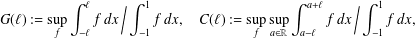$$\begin{eqnarray}G(\ell ):=\sup _{f}\int _{-\ell }^{\ell }f\,dx\,\bigg/\int _{-1}^{1}f\,dx,\quad C(\ell ):=\sup _{f}\sup _{a\in \mathbb{R}}\int _{a-\ell }^{a+\ell }f\,dx\,\bigg/\int _{-1}^{1}f\,dx,\end{eqnarray}$$
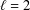where the supremum is taken over all not identically zero nonnegative positive definite functions. We investigate how large these extremal quantities can be. This problem was originally posed by Yu. Shteinikov and S. Konyagin (for the case $\ell =2$) and is an extension of the classical problem of Wiener. In this note we obtain exact values for the right limits 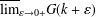$\overline{\lim }_{\unicode[STIX]{x1D700}\rightarrow 0+}G(k+\unicode[STIX]{x1D700})$ and 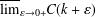$\overline{\lim }_{\unicode[STIX]{x1D700}\rightarrow 0+}C(k+\unicode[STIX]{x1D700})$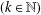$(k\in \mathbb{N})$ taken over doubly positive functions, and sufficiently close bounds for other values of 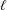$\ell$.

Keywords

nonnegative positive definite functionWiener’s problemSchur’s theoremFourier transformconvolution square

MSC classification

Primary: 42A82: Positive definite functions
Secondary: 26D15: Inequalities for sums, series and integrals 42A38: Fourier and Fourier-Stieltjes transforms and other transforms of Fourier type
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 1 , August 2017 , pp. 117 - 125
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author was supported by the Russian Foundation for Basic Research (project no. 15-01-02705) and by the Program for State Support of Leading Scientific Schools of the Russian Federation (project no. NSh-9356.2016.1). The first and third authors were supported by the Competitiveness Enhancement Program of the Ural Federal University (Enactment of the Government of the Russian Federation of 16 March 2013 no. 211, agreement no. 02.A03.21.0006 of 27 August 2013). The second author was supported by the ‘Lendület’ Program (LP2012-46/2012) of the Hungarian Academy of Sciences and the National Research, Development and Innovation Office, NKFIH Reg. no. K115383. The third author was supported by Hungarian Science Foundation Grant nos. NK-104183, K-109789.

References

Bonami, A. and Révész, Sz. Gy., ‘Failure of Wiener’s property for positive definite periodic functions’, C. R. Math. Acad. Sci. Paris 346(1–2) (2008), 39–44.CrossRefGoogle Scholar
Cohn, H., ‘New upper bounds on sphere packings. II’, Geom. Topol. 6 (2002), 329–353.CrossRefGoogle Scholar
Cohn, H. and Elkies, N., ‘New upper bounds on sphere packings. I’, Ann. of Math. (2) 157(2) (2003), 689–714.CrossRefGoogle Scholar
Cohn, H., Kumar, A., Miller, S., Radchenko, D. and Viazovska, M., ‘The sphere packing problem in dimension 24’, Annals of Math., to appear, arXiv:1603.06518.Google Scholar
Ehm, W., Gneiting, T. and Richards, D., ‘Convolution roots of radial positive definite functions with compact support’, Trans. Amer. Math. Soc. 356(11) (2004), 4655–4685.CrossRefGoogle Scholar
Gorbachev, D. V., ‘Extremal problem for entire functions of exponential spherical type, connected with the Levenshtein bound on the sphere packing density in ℝ n ’, Izv. Tula State Univ. Ser. Math. Mech. Inform. 6 (2000), 71–78 (in Russian).Google Scholar
Gorbachev, D. V., ‘Certain inequalities for discrete, nonnegative, positive definite functions’, Izv. Tulskogo Univ. Estestv. Nauki 2015(2) (2015), 1–8 (in Russian).Google Scholar
Gorbachev, D. V. and Tikhonov, S. Yu., ‘Doubling condition at the origin for non-negative positive definite functions’, Preprint, 2016, arXiv:1612.08637.Google Scholar
Gorbachev, D. V. and Tikhonov, S. Yu., ‘Wiener’s problem for positive definite functions’, Preprint, 2016, arXiv:1604.01302.Google Scholar
Ivanov, V. I., ‘On the Turán and Delsarte problems for periodic positive-definite functions’, Mat. Zametki 80(6) (2006), 934–939 (in Russian), translation in Math. Notes 80(5–6) (2006), 875–880.Google Scholar
Révész, Sz. Gy., Extremal Problems for Positive Definite Functions and Polynomials, Thesis for the degree of Doctor of the Academy, Budapest, 2009, 164 pages.Google Scholar
Révész, Sz. Gy., ‘Turán’s extremal problem on locally compact abelian groups’, Anal. Math. 37(1) (2011), 15–50.CrossRefGoogle Scholar
Shapiro, H. S., ‘Majorant problems for Fourier coefficients’, Quart. J. Math. Oxford, Ser. (2) 26 (1975), 9–18.CrossRefGoogle Scholar
Shteinikov, Yu. N., ‘On the set of joint representatives of two congruence classes’, Trudy Matematicheskogo Instituta imeni V.A. Steklova 290 (2015), 202–210 (in Russian); translation in Proc. Steklov Institute of Mathematics 290 (2015), 189–196.Google Scholar
Viazovska, M., ‘The sphere packing problem in dimension 8’, Annals of Math., to appear, arXiv:1603.04246.Google Scholar
Wainger, S., ‘A problem of Wiener and the failure of a principle for Fourier series with positive coefficients’, Proc. Amer. Math. Soc. 20 (1969), 16–18.CrossRefGoogle Scholar
Wiener, N., ‘A class of gap theorems’, Ann. Sc. Norm. Super. Pisa (2) 3 (1934), 367–372.Google Scholar