Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T11:51:34.829Z Has data issue: false hasContentIssue false
  • English
  • Français

ON HYPERSTABILITY OF ADDITIVE MAPPINGS ONTO BANACH SPACES

Part of: Normed linear spaces and Banach spaces; Banach lattices Nonlinear operators and their properties

Published online by Cambridge University Press:  30 December 2014

YUNBAI DONG  and
BENTUO ZHENG
YUNBAI DONG*
Affiliation:
School of Mathematics and Computer, Wuhan Textile University, Wuhan 430073, China email [email protected]
BENTUO ZHENG
Affiliation:
Department of Mathematical Sciences, The University of Memphis, Memphis, TN 38152-3240, USA email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 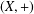$(X,+)$ be an Abelian group and $E$ be a Banach space. Suppose that 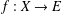$f:X\rightarrow E$ is a surjective map satisfying the inequality

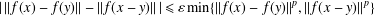$$\begin{eqnarray}|\,\Vert f(x)-f(y)\Vert -\Vert f(x-y)\Vert \,|\leq {\it\varepsilon}\min \{\Vert f(x)-f(y)\Vert ^{p},\Vert f(x-y)\Vert ^{p}\}\end{eqnarray}$$
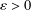for some ${\it\varepsilon}>0$, 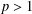$p>1$ and for all 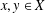$x,y\in X$. We prove that $f$ is an additive map. However, this result does not hold for 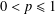$0<p\leq 1$. As an application, we show that if 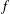$f$ is a surjective map from a Banach space 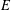$E$ onto a Banach space 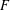$F$ so that for some 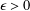${\it\epsilon}>0$ and 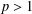$p>1$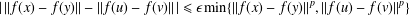
$$\begin{eqnarray}|\,\Vert f(x)-f(y)\Vert -\Vert f(u)-f(v)\Vert \,|\leq {\it\epsilon}\min \{\Vert f(x)-f(y)\Vert ^{p},\Vert f(u)-f(v)\Vert ^{p}\}\end{eqnarray}$$
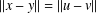 whenever $\Vert x-y\Vert =\Vert u-v\Vert$, then 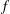$f$ preserves equality of distance. Moreover, if 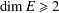$\dim E\geq 2$, there exists a constant 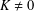$K\neq 0$ such that 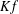$Kf$ is an affine isometry. This improves a result of Vogt [‘Maps which preserve equality of distance’, Studia Math.45 (1973) 43–48].

Keywords

hyperstabilityBanach spacesadditive mappingsfunctional equations

MSC classification

Primary: 39B82: Stability, separation, extension, and related topics
Secondary: 46B04: Isometric theory of Banach spaces 47H14: Perturbations of nonlinear operators
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 91 , Issue 2 , April 2015 , pp. 278 - 285
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Bahyrycz, A. and Piszczek, M., ‘Hyperstability of the Jensen functional equation’, Acta Math. Hungar. 142(2) (2014), 353–365.Google Scholar
Benyamini, Y. and Lindenstrauss, J., Geometric Nonlinear Functional Analysis, Vol. 1, Colloquium Publications, 48 (American Mathematical Society, Providence, RI, 2000).Google Scholar
Bourgin, D. G., ‘Approximately isometric and multiplicative transformations on continuous function rings’, Duke Math. J. 16 (1949), 385–397.Google Scholar
Brzdȩk, J., ‘Hyperstability of the Cauchy equation on restricted domains’, Acta Math. Hungar. 141(1–2) (2013), 58–67.CrossRefGoogle Scholar
Brzdȩk, J., ‘Remarks on hyperstability of the Cauchy functional equation’, Aequationes Math. 86 (2013), 255–267.Google Scholar
Brzdȩk, J., ‘A hyperstability result for the Cauchy equation’, Bull. Aust. Math. Soc. 89 (2014), 33–40.CrossRefGoogle Scholar
Brzdȩk, J. and Ciepliński, K., ‘Hyperstability and superstability’, Abstr. Appl. Anal. 2013 (2013), Article ID 401756, 13 pages.Google Scholar
Brzdȩk, J., Najdecki, A. and Xu, B., ‘Two general theorems on superstability of functional equations’, Aequationes Math., to appear. Published online (12 June 2014).Google Scholar
Dong, Y., ‘Generalized stabilities of two functional equations’, Aequationes Math. 86 (2013), 269–277.Google Scholar
Ger, R., ‘A Pexider-type equation in normed linear spaces’, Österreich. Akad. Wiss. Math.-Natur. Kl. Sitzungsber. II 206 (1997), 291–303.Google Scholar
Hu, R., ‘On the maps preserving the equality of distance’, J. Math. Anal. Appl. 343 (2008), 1161–1165.Google Scholar
Hyers, D. H., ‘On the stability of the linear functional equation’, Proc. Natl. Acad. Sci. 27 (1941), 222–224.Google Scholar
John, F., ‘On quasi-isometric mappings, I’, Comm. Pure Appl. Math. 21 (1968), 77–110.Google Scholar
Jung, S. M., Hyers–Ulam–Rassias Stability of Functional Equations in Nonlinear Analysis, Springer Optimization and its Applications, 48 (Springer, New York, 2011).Google Scholar
Omladič, M. and Šemrl, P., ‘On non linear perturbations of isometries’, Math. Ann. 303 (1995), 617–628.CrossRefGoogle Scholar
Piszczek, M., ‘Remark on hyperstability of the general linear equation’, Aequationes Math. 88 (2014), 163–168.CrossRefGoogle Scholar
Rassias, Th. M., ‘On the stability of the linear mapping in Banach spaces’, Proc. Amer. Math. Soc. 72 (1978), 297–300.Google Scholar
Rassias, Th. M., ‘On the stability of functional equations in Banach space’, J. Math. Anal. Appl. 251 (2000), 264–284.Google Scholar
Sikorska, J., ‘Stability of the preservation of the equality of distance’, J. Math. Anal. Appl. 311 (2005), 209–217.Google Scholar
Skof, F., ‘On the functional equation ∥f (x + y) − f (x)∥ = ∥f (y)∥’, Atti Accad. Sci. Torino Cl. Sci. Fis. Mat. Natur. 127 (1993), 229–237.Google Scholar
Vogt, A., ‘Maps which preserve equality of distance’, Studia Math. 45 (1973), 43–48.Google Scholar