Let f ∈ ℤ[X] and let q be a prime power pl(l ≥ 2). Hua stated and proved that

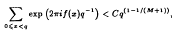
for some unspecified constant C > 0 depending on the derivative f′ of f; M denoting the maximum multiplicity of the roots of the congruence p−tf′(x) ≡ 0 (mod p), where t is an integer chosen so that the polynomial p−tf′(x) is primitive. An explicit value for C was given by Chalk for p ≥ 3. Subsequently, Ping Ding (in two successive articles) obtained better estimates for p ≥ 2.

This article provides a better result, based upon a more precise form of Hua's main lemma, previously overlooked.