Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Frankl, P.
1978.
An extremal problem for 3-graphs.
Acta Mathematica Academiae Scientiarum Hungaricae,
Vol. 32,
Issue. 1-2,
p.
157.
Frankl, P.
1980.
Families of finite sets with prescribed cardinalities for pairwise intersections.
Acta Mathematica Academiae Scientiarum Hungaricae,
Vol. 35,
Issue. 3-4,
p.
351.
Frankl, Peter
1980.
On intersecting families of finite sets.
Bulletin of the Australian Mathematical Society,
Vol. 21,
Issue. 3,
p.
363.
Frankl, P.
1980.
Extremal Problems and Coverings of the Space.
European Journal of Combinatorics,
Vol. 1,
Issue. 2,
p.
101.
Burr, Stefan A.
and
Duke, Richard A.
1981.
Ramsey numbers for certain k-graphs.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 30,
Issue. 3,
p.
284.
Erdős, P.
1981.
On the combinatorial problems which I would most like to see solved.
Combinatorica,
Vol. 1,
Issue. 1,
p.
25.
West, Douglas B.
1982.
Ordered Sets.
p.
473.
Deza, M.
and
Frankl, P.
1983.
Erdös–Ko–Rado Theorem—22 Years Later.
SIAM Journal on Algebraic Discrete Methods,
Vol. 4,
Issue. 4,
p.
419.
Frankl, P.
and
Singhi, N.M.
1983.
Linear Dependencies among Subsets of a Finite Set.
European Journal of Combinatorics,
Vol. 4,
Issue. 4,
p.
313.
Frankl, Peter
1983.
An extremal set theoretical characterization of some steiner systems.
Combinatorica,
Vol. 3,
Issue. 2,
p.
193.
Frankl, Peter
and
Füredi, Zoltán
1983.
A new generalization of the Erdős-Ko-Rado theorem.
Combinatorica,
Vol. 3,
Issue. 3-4,
p.
341.
FRANKL, P.
and
FÜREDI, Z.
1984.
Finite and Infinite Sets.
p.
305.
Frankl, Peter
and
Füredi, Zoltán
1985.
Forbidding just one intersection.
Journal of Combinatorial Theory, Series A,
Vol. 39,
Issue. 2,
p.
160.
Erdös, P.
1985.
PROBLEMS AND RESULTS IN COMBINATORIAL GEOMETRYa.
Annals of the New York Academy of Sciences,
Vol. 440,
Issue. 1,
p.
1.
Füredi, Zoltán
Hwang, Kyung-Won
and
Weichsel, Paul M.
2006.
Topics in Discrete Mathematics.
Vol. 26,
Issue. ,
p.
215.
Keevash, Peter
Mubayi, Dhruv
and
Wilson, Richard M.
2006.
Set Systems with No Singleton Intersection.
SIAM Journal on Discrete Mathematics,
Vol. 20,
Issue. 4,
p.
1031.
Füredi, Zoltán
2011.
Linear paths and trees in uniform hypergraphs.
Electronic Notes in Discrete Mathematics,
Vol. 38,
Issue. ,
p.
377.
Füredi, Zoltán
and
Jiang, Tao
2014.
Hypergraph Turán numbers of linear cycles.
Journal of Combinatorial Theory, Series A,
Vol. 123,
Issue. 1,
p.
252.
Füredi, Zoltán
Jiang, Tao
and
Seiver, Robert
2014.
Exact solution of the hypergraph Turán problem for k-uniform linear paths.
Combinatorica,
Vol. 34,
Issue. 3,
p.
299.
Füredi, Zoltán
2014.
Linear trees in uniform hypergraphs.
European Journal of Combinatorics,
Vol. 35,
Issue. ,
p.
264.


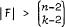 then we can find two members
then we can find two members 