Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T17:05:53.178Z Has data issue: false hasContentIssue false
  • English
  • Français

ON EXTENSIONS OF THE GENERALISED JENSEN FUNCTIONS ON SEMIGROUPS

Published online by Cambridge University Press:  13 February 2017

JANUSZ BRZDĘK  and
ELIZA JABŁOŃSKA
JANUSZ BRZDĘK
Affiliation:
Department of Mathematics, Pedagogical University, Podchorążych 2, 30-084 Kraków, Poland email [email protected]
ELIZA JABŁOŃSKA*
Affiliation:
Department of Discrete Mathematics, Rzeszów University of Technology, Powstańców Warszawy 12, 35-959 Rzeszów, Poland email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Assume that 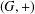$(G,+)$ is a commutative semigroup, $\unicode[STIX]{x1D70F}$ is an endomorphism of 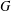$G$ and an involution, 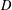$D$ is a nonempty subset of 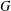$G$ and 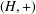$(H,+)$ is an abelian group uniquely divisible by two. We prove that if 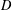$D$ is ‘sufficiently large’, then each function 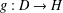$g:D\rightarrow H$ satisfying 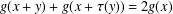$g(x+y)+g(x+\unicode[STIX]{x1D70F}(y))=2g(x)$ for 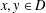$x,y\in D$ with 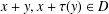$x+y,x+\unicode[STIX]{x1D70F}(y)\in D$ can be extended to a unique solution 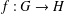$f:G\rightarrow H$ of the generalised Jensen functional equation 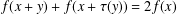$f(x+y)+f(x+\unicode[STIX]{x1D70F}(y))=2f(x)$.

Keywords

Jensen functionrestricted domainabelian semigroupinvolutionfilter

MSC classification

Primary: 39B52: Equations for functions with more general domains and/or ranges
Secondary: 39B82: Stability, separation, extension, and related topics
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 1 , August 2017 , pp. 110 - 116
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Aczél, J., ‘“Remark 5” in the report of the meeting of the forty-second international symposium on functional equations (June 20–27, 2004, Opava, Czech Republic)’, Aequationes Math. 69 (2005), 164–200.Google Scholar
Bahyrycz, A., Brzdęk, J. and Jabłońska, E., ‘Extensions of the generalized cosine functions’, Publ. Math. Debrecen 89 (2016), 263–275.CrossRefGoogle Scholar
Baron, K., ‘On additive involutions and Hamel bases’, Aequationes Math. 87(1–2) (2014), 159–163.CrossRefGoogle Scholar
de Bruijn, N. G., ‘On almost additive mappings’, Colloq. Math. 15 (1966), 59–63.Google Scholar
Brzdęk, J., ‘On almost additive mappings’, Bull. Aust. Math. Soc. 54 (1996), 281–290.Google Scholar
Christensen, J. P. R., ‘On sets of Haar measure zero in abelian Polish groups’, Israel J. Math. 13 (1972), 255–260.CrossRefGoogle Scholar
Darji, U. B., ‘On Haar meager sets’, Topology Appl. 160 (2013), 2396–2400.CrossRefGoogle Scholar
Fischer, P. and Słodkowski, Z., ‘Christensen zero sets and measurable convex functions’, Proc. Amer. Math. Soc. 79 (1980), 449–453.Google Scholar
Ger, R., ‘On almost polynomial functions’, Colloq. Math. 24 (1971), 95–101.Google Scholar
Ger, R., ‘Note on almost additive functions’, Aequationes Math. 17 (1978), 73–76.CrossRefGoogle Scholar
Hartman, S., ‘A remark about Cauchy’s equation’, Colloq. Math. 8 (1961), 77–79.Google Scholar
Jurkat, W. B., ‘On Cauchy’s functional equation’, Proc. Amer. Math. Soc. 16 (1965), 683–696.Google Scholar
Kuczma, M., An Introduction to the Theory of Functional Equations and Inequalities (Państwowe Wydawnictwo Naukowe and Uniwersytet Śląski, Warszawa–Kraków–Katowice, 1985).Google Scholar
Sinopoulos, P., ‘Functional equations on semigroups’, Aequationes Math. 59 (2000), 255–261.CrossRefGoogle Scholar
Stetkær, H., ‘Functional equation on abelian groups with involution’, Aequationes Math. 54 (1997), 144–172.Google Scholar
Stetkær, H., Functional Equations on Groups (World Scientific Publishing Company, Singapore, 2013).Google Scholar