Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-20T09:38:17.412Z Has data issue: false hasContentIssue false
  • English
  • Français

ON EXPONENTIAL DIOPHANTINE EQUATIONS CONTAINING THE EULER QUOTIENT

Part of: Diophantine equations

Published online by Cambridge University Press:  14 October 2014

NOBUHIRO TERAI
NOBUHIRO TERAI*
Affiliation:
Department of Computer Science and Intelligent Systems, Faculty of Engineering, Oita University, 700 Dannoharu, Oita 870-1192, Japan email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

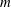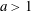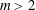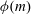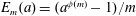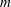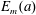Let $a$ and $m$ be relatively prime positive integers with $a>1$ and $m>2$. Let ${\it\phi}(m)$ be Euler’s totient function. The quotient $E_{m}(a)=(a^{{\it\phi}(m)}-1)/m$ is called the Euler quotient of $m$ with base $a$. By Euler’s theorem, $E_{m}(a)$ is an integer. In this paper, we consider the Diophantine equation 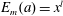$E_{m}(a)=x^{l}$ in integers 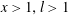$x>1,l>1$. We conjecture that this equation has exactly five solutions 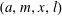$(a,m,x,l)$ except for 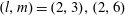$(l,m)=(2,3),(2,6)$, and show that if the equation has solutions, then 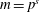$m=p^{s}$ or 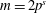$m=2p^{s}$ with 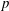$p$ an odd prime and 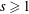$s\geq 1$.

Keywords

exponential Diophantine equationsFermat quotientEuler quotientinteger solutions

MSC classification

Primary: 11D61: Exponential equations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 91 , Issue 1 , February 2015 , pp. 11 - 18
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Agoh, T., Dilcher, K. and Skula, L., ‘Fermat quotients for composite moduli’, J. Number Theory 66 (1997), 29–50.CrossRefGoogle Scholar
Bennett, M. A. and Skinner, C., ‘Ternary Diophantine equations via Galois representations and modular forms’, Canad. J. Math. 56 (2004), 23–54.Google Scholar
Bennett, M. A., Vatsal, V. and Yazdani, S., ‘Ternary Diophantine equations of signature (p, p, 3)’, Compositio Math. 140 (2004), 1399–1416.CrossRefGoogle Scholar
Bosma, W. and Cannon, J., Handbook of Magma Functions, Department of Mathematics, University of Sydney, available online at http://magma.maths.usyd.edu.au/magma/.Google Scholar
Cao, Z., ‘The Diophantine equations x 4 − y 4 = z p and x 4 − 1 = d y q’, C. R. Math. Rep. Acad. Sci. Can. 21 (1999), 23–27.Google Scholar
Cohn, J.H.E., ‘The Diophantine equations x 4 − D y 2 = 1, II’, Acta Arith. 78 (1996/1997), 401–403.CrossRefGoogle Scholar
Dickson, L.E., History of the Theory of Numbers, Vol. I (Chelsea, New York, 1971).Google Scholar
Kihel, O. and Levesque, C., ‘On a few Diophantine equations related to Fermat’s last theorem’, Canad. Math. Bull. 45 (2002), 247–256.Google Scholar
Le, M. H., ‘A note on the Diophantine equation x p−1 − 1 = p y q’, C. R. Math. Rep. Acad. Sci. Can. 15 (1993), 121–124.Google Scholar
Ljunggren, W., ‘Zur Theorie der Gleichung x 2 + 1 = D y 4’, Avh. Norske Vid. Akad. Oslo 5 (1942), 1–27.Google Scholar
Lucas, E., Théorie des nombres (Gauthier-Villars, Paris, 1891), reprinted (A. Blanchard, Paris, 1961).Google Scholar
Mihilescu, P., ‘Primary cyclotomic units and a proof of Catalan’s conjecture’, J. reine angew. Math. 572 (2004), 167–195.Google Scholar
Nagell, T., Introduction to Number Theory, 2nd edn (Chelsea, New York, 1964).Google Scholar
Osada, H. and Terai, N., ‘Generalization of Lucas’ Theorem for Fermat’s quotient’, C. R. Math. Rep. Acad. Sci. Can. 11 (1989), 115–120.Google Scholar
Störmer, C., ‘L’équation m arctan1∕x + n arctan1∕y = k𝜋∕4’, Bull. Soc. Math. France 27 (1899), 160–170.CrossRefGoogle Scholar
Terai, N., ‘Generalization of Lucas’ Theorem for Fermat’s quotient II’, Tokyo J. Math. 13 (1990), 277–287.Google Scholar