Hostname: page-component-6bf8c574d5-956mj Total loading time: 0 Render date: 2025-02-16T19:02:59.988Z Has data issue: false hasContentIssue false
  • English
  • Français

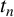ON DISCRIMINANTS OF MINIMAL POLYNOMIALS OF THE RAMANUJAN $t_n$ CLASS INVARIANTS

Part of: Discontinuous groups and automorphic forms Arithmetic algebraic geometry Algebraic number theory: global fields

Published online by Cambridge University Press:  11 April 2023

SARTH CHAVAN Open the ORCID record for SARTH CHAVAN [Opens in a new window]
SARTH CHAVAN*
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA, USA e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the discriminants of the minimal polynomials 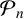$\mathcal {P}_n$ of the Ramanujan 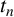$t_n$ class invariants, which are defined for positive 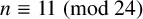$n\equiv 11\pmod {24}$. We show that 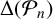$\Delta (\mathcal {P}_n)$ divides 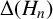$\Delta (H_n)$, where 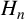$H_n$ is the ring class polynomial, with quotient a perfect square and determine the sign of 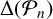$\Delta (\mathcal {P}_n)$ based on the ideal class group structure of the order of discriminant 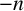$-n$. We also show that the discriminant of the number field generated by 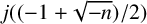$j({(-1+\sqrt {-n})}/{2})$, where j is the j-invariant, divides 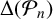$\Delta (\mathcal {P}_n)$. Moreover, using Ye’s computation of 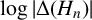$\log|\Delta(H_n)|$ [‘Revisiting the Gross–Zagier discriminant formula’, Math. Nachr. 293 (2020), 1801–1826], we show that 3 never divides 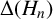$\Delta(H_n)$, and thus 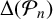$\Delta(\mathcal{P}_n)$, for all squarefree 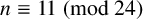$n\equiv11\pmod{24}$.

Keywords

elliptic curvesring class polynomialsclass invariantj-invariantdiscriminant

MSC classification

Primary: 11R29: Class numbers, class groups, discriminants
Secondary: 11F03: Modular and automorphic functions 11G07: Elliptic curves over local fields 11R09: Polynomials (irreducibility, etc.) 11R37: Class field theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 108 , Issue 2 , October 2023 , pp. 264 - 275
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author was supported by The 2022 Spirit of Ramanujan Fellowship and The 2022 Mehta Fellowship.

Dedicated to all my Rickoid friends who turned into a family

References

Atkin, A. O. L. and Morain, F., ‘Elliptic curves and primality proving’, Math. Comp. 61 (1993), 29–68.10.1090/S0025-5718-1993-1199989-XCrossRefGoogle Scholar
Berndt, B. C. and Chan, H. H., ‘Ramanujan and the modular $j$ -invariant’, Canad. Math. Bull. 42(4) (1999), 427–440.10.4153/CMB-1999-050-1CrossRefGoogle Scholar
Bröker, R. and Stevenhagen, P., ‘Efficient CM-constructions of elliptic curves over finite fields’, Math. Comp. 76 (2007), 2161–2179.10.1090/S0025-5718-07-01980-1CrossRefGoogle Scholar
Cox, D. A., Primes of the Form ${x}^2+n{y}^2$ , 2nd edn (John Wiley and Sons, Hoboken, NJ, 2013).Google Scholar
Dorman, D. R., ‘Singular moduli, modular polynomials, and the index of the closure of $\mathbb{Z}\left[j\left(\tau \right)\right]$ in $\mathbb{Q}\left(j\left(\tau \right)\right)$ ’, Math. Ann. 283 (1989), 177–191.10.1007/BF01446429CrossRefGoogle Scholar
Gross, B. H. and Zagier, D. B., ‘On singular moduli’, J. reine angew. Math. 355 (1985), 191–220.Google Scholar
Konstantinou, E. and Kontogeorgis, A., ‘Computing polynomials of the Ramanujan ${t}_n$ class invariants’, Canad. Math. Bull. 52(4) (2009), 583–597.10.4153/CMB-2009-058-6CrossRefGoogle Scholar
Konstantinou, E. and Kontogeorgis, A., ‘Ramanujan’s class invariants and their use in elliptic curve cryptography’, Comput. Math. Appl. 59(8) (2010), 2901–2917.10.1016/j.camwa.2010.02.008CrossRefGoogle Scholar
Miyaji, A., Nakabayashi, M. and Takano, S., ‘New explicit conditions of elliptic curve traces for FR-reduction’, IEICE Trans. Fundam. Electron., Commun. Comput. Sci. E84‐A(5) (2001), 1234–1243.Google Scholar
Neukirch, J., Algebraic Number Theory (Springer, Berlin–Heidelberg, 1999).10.1007/978-3-662-03983-0CrossRefGoogle Scholar
Ramanujan, S., Notebooks, Vols. 1, 2 (TIFR, Bombay, 1957).Google Scholar
Scott, M. and Barreto, P. S. L. M., ‘Generating more MNT elliptic curves’, Des. Codes Cryptogr. 38 (2006), 209–217.10.1007/s10623-005-0538-1CrossRefGoogle Scholar
Stein, W., Sage Mathematics Software, Sage Development Team (2021). Available online at http://www.sagemath.org.Google Scholar
Ye, D., ‘Revisiting the Gross–Zagier discriminant formula’, Math. Nachr. 293 (2020), 1801–1826.10.1002/mana.201900298CrossRefGoogle Scholar