Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-25T05:47:40.621Z Has data issue: false hasContentIssue false
  • English
  • Français

On closed radical orbits in homogeneous complex manifolds

Published online by Cambridge University Press:  17 April 2009

Bruce Gilligan
Bruce Gilligan
Affiliation:
Department of Mathematics and Statistics, University of Regina Regina, Canada S4S 0A2, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose G is a complex Lie group having a finite number of connected components and H is a closed complex subgroup of G with H° solvable. Let RG denote the radical of G. We show the existence of closed complex subgroups I and J of G containing H such that I/H is a connected solvmanifold with I° ⊃ RG, the space G/J has a Klein form SG/A, where A is an algebraic subgroup of the semisimple complex Lie group SG: = G/RG, and, unless I = J, the space J/I has Klein form 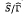, where 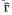is a Zariski dense discrete subgroup of some connected positive dimensional semisimple complex Lie group Ŝ.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 54 , Issue 3 , December 1996 , pp. 363 - 368
Copyright
Copyright © Australian Mathematical Society 1996

References

[1]Auslander, L., ‘On radicals of discrete subgroups of Lie groups’, Amer. J. Math. 85 (1963), 145–150.CrossRefGoogle Scholar
[2]Auslander, L. and Tolimieri, R., ‘Splitting theorems and the structure of solvmanifolds’, Ann. of Math. 92 (1970), 164–173.CrossRefGoogle Scholar
[3]Chevalley, C., Théorie des groupes de Lie II: Groupes algébriques (Hermann, Paris, 1951).Google Scholar
[4]Gilligan, B., ‘Ends of complex homogeneous manifolds having non–constant holomorphic functions’, Arch. Math. 37 (1981), 544–555.CrossRefGoogle Scholar
[5]Gilligan, B. and Heinzner, P., ‘Globalization of holomorphic actions on principal bundles’, (preprint, 1995).Google Scholar
[6]Gorbatsevich, V. V. and Onishchik, A. L., ‘Lie groups of transformations’, (in Russian), in Current problems in mathematics, Fundamental directions. 20, pp. 103–238. Moscow, 1988; Engl. transl. in Enclyclopaedia of Mathematical Sciences, 20 (Springer-Verlag, 1993) 95–229.Google Scholar
[7]Huckleberry, A. T. and Oeljeklaus, E., ‘Homogeneous spaces from a complex analytic viewpoint’, in Manifolds and Lie groups. (Papers in honor of Y. Matsushima), Progress in Math. (Birkhäuser, Boston, 1981), pp. 159–186.CrossRefGoogle Scholar
[8]Karpelevich, F.I., ‘On a fibration of homogeneous spaces’, (in Russian), Uspekhi Mat. Nauk 11 (1956), 131–138.Google Scholar
[9]Mostow, G.D., ‘On covariant fiberings of Klein spaces, I, II’, Amer. J. Math. 77 (1955), 247–278. 84 (1962) 466–474.CrossRefGoogle Scholar
[10]Mostow, G.D., ‘Some applications of representative functions to solv-manifolds’, Amer. J. Math. 93 (1971), 11–32.CrossRefGoogle Scholar
[11]Wang, H-C., ‘On the deformations of lattices in a Lie group’, Amer. J. Math. 85 (1963), 189–212.CrossRefGoogle Scholar