Let Qp and K be the rational p–adic field and an algebraic extension of Qp of finite degree, respectively, and let I and Ik be the subsets of Qp and of K consisting of the p–adic integers of these fields.

It is known that the continuous functions f: I → Qp can be written as

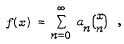
where this series converges uniformly on I, and that such continuous functions need not be differentiable at any point. We here study continuous functions F: IK → K which for all X on IK are the sum of a uniformly convergent series

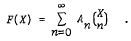
It is proved that such functions F(X) have at every point of IK derivatives of all orders. In the special case when K is totally ramified, they cannot in general be developed into power series that converge everywhere on IK, but this is possible when K is not totally ramified.