No CrossRef data available.
Article contents
On bounds for the Lipschitz constant of the remainder in polynomial approximation
Published online by Cambridge University Press: 17 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Suppose f is a function possessing a kth order derivative, the derivative being Lipschitz continuous of order α, 0 < α ≤ 1, on [−1, 1]. Let Pn be a polynomial of degree ≤ n approximating to f on [−1,1] such that if rn = f − Pn then ∥rn∥∞ ≤ An−k−a Define
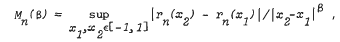
where 0 < β ≤ 1. Upper bounds are obtained for Mn(β) when k ≥ 1 thereby generalizing results previously given for functions which are only Lipschitz continuous on [−1,1].
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1986
References
[1]Ioakimidis, N.I., “An improvement of Kalandiya's theorem”, J. Approx. Theory 38 (1983), 354–356.CrossRefGoogle Scholar
[2]Kalandiya, A.I., “On a direct method of solution of an equation in wing theory and its application to the theory of elasticity”, Mat. Sb. 42 (1957), 249–272. (In Russian)
Google Scholar
[3]Meinardus, G., Approximation of functions: theory and nwnerical methods, (Springer–verlag, Berlin, Heidelberg, New York, 1967).
CrossRefGoogle Scholar
[4]Stečkin, S.B., “Generalization of some Bernstein inequalities”, Dok l. Akad. Nauk SSSR 60 (1948), 1511–1514. (In Russian).Google Scholar
You have
Access