Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Matala-aho, Tapani
and
Prévost, Marc
2002.
Irrationality Measures for the Series of Reciprocals from Recurrence Sequences.
Journal of Number Theory,
Vol. 96,
Issue. 2,
p.
275.
Зудилин, Вадим Валентинович
and
Zudilin, Wadim Valentinovich
2002.
О диофантовых задачах для $q$-дзета-значений.
Математические заметки,
Vol. 72,
Issue. 6,
p.
936.
TACHIYA, Yohei
2004.
Irrationality of Certain Lambert Series.
Tokyo Journal of Mathematics,
Vol. 27,
Issue. 1,
Matala-aho, Tapani
Väänänen, Keijo
and
Zudilin, Wadim
2005.
New irrationality measures for 𝑞-logarithms.
Mathematics of Computation,
Vol. 75,
Issue. 254,
p.
879.
Matala-aho, Tapani
2008.
On irrationality measures of ∑l=0∞dl/∏j=1l(1+djr+d2js).
Journal of Number Theory,
Vol. 128,
Issue. 1,
p.
1.
Coussement, J.
and
Smet, C.
2009.
Irrationality proof of certain Lambert series using little q-Jacobi polynomials.
Journal of Computational and Applied Mathematics,
Vol. 233,
Issue. 3,
p.
680.
Amano, Kenji
and
Tachiya, Yohei
2009.
On the irrationality measure for certain series.
Monatshefte für Mathematik,
Vol. 156,
Issue. 1,
p.
1.
Rochev, Igor P
2011.
On linear independence of values of certain $ q$-series.
Izvestiya: Mathematics,
Vol. 75,
Issue. 1,
p.
177.
Рочев, Игорь Петрович
and
Rochev, Igor Petrovich
2011.
О линейной независимости значений некоторых $q$-рядов.
Известия Российской академии наук. Серия математическая,
Vol. 75,
Issue. 1,
p.
181.
Mansour, Toufik
and
Shattuck, Mark
2014.
A $$q$$ -analog of the hyperharmonic numbers.
Afrika Matematika,
Vol. 25,
Issue. 1,
p.
147.
ÇETİN, Miraç
KIZILATEŞ, Can
YEŞİL BARAN, Fatma
and
TUGLU, Naim
2021.
Some Identities of Harmonic and Hyperharmonic Fibonacci Numbers.
Gazi University Journal of Science,
Vol. 34,
Issue. 2,
p.
493.
Duverney, Daniel
and
Tachiya, Yohei
2023.
Linear independence of certain sums of reciprocals of the Lucas numbers.
Periodica Mathematica Hungarica,
Vol. 86,
Issue. 2,
p.
378.


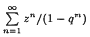 we obtain new approximation measures for values of
we obtain new approximation measures for values of 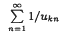 ,
,