Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T09:59:05.743Z Has data issue: false hasContentIssue false
  • English
  • Français

ON APPROXIMATELY ADDITIVE MAPPINGS IN 2-BANACH SPACES

Part of: Nonlinear operators and their properties

Published online by Cambridge University Press:  15 August 2019

JANUSZ BRZDĘK Open the ORCID record for JANUSZ BRZDĘK [Opens in a new window]  and
EL-SAYED EL-HADY Open the ORCID record for EL-SAYED EL-HADY [Opens in a new window]
JANUSZ BRZDĘK*
Affiliation:
Faculty of Applied Mathematics, AGH University of Science and Technology, Mickiewicza 30, 30-059 Kraków, Poland email [email protected]
EL-SAYED EL-HADY
Affiliation:
Mathematics Department, College of Science, Jouf University, PO Box 2014, Sakaka, Saudi Arabia Basic Science Department, Faculty of Computers and Informatics, Suez Canal University, Ismailia, 41522, Egypt email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

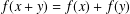We show how some Ulam stability issues can be approached for functions taking values in 2-Banach spaces. We use the example of the well-known Cauchy equation $f(x+y)=f(x)+f(y)$, but we believe that this method can be applied for many other equations. In particular we provide an extension of an earlier stability result that has been motivated by a problem of Th. M. Rassias. The main tool is a recent fixed point theorem in some spaces of functions with values in 2-Banach spaces.

Keywords

Cauchy equationUlam stability2-Banach space2-norm

MSC classification

Primary: 39B82: Stability, separation, extension, and related topics
Secondary: 39B52: Equations for functions with more general domains and/or ranges 47H10: Fixed-point theorems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 2 , April 2020 , pp. 299 - 310
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agarwal, R. P., Xu, B. and Zhang, W., ‘Stability of functional equations in single variable’, J. Math. Anal. Appl. 288(2) (2003), 852–869.Google Scholar
Bahyrycz, A. and Olko, J., ‘On stability of the general linear equation’, Aequationes Math. 89(6) (2015), 1461–1474.Google Scholar
Bahyrycz, A. and Olko, J., ‘Hyperstability of general linear functional equation’, Aequationes Math. 90(3) (2016), 527–540.Google Scholar
Bahyrycz, A. and Piszczek, M., ‘Hyperstability of the Jensen functional equation’, Acta Math. Hungar. 142(2) (2014), 353–365.Google Scholar
Brzdęk, J., ‘Hyperstability of the Cauchy equation on restricted domains’, Acta Math. Hungar. 141(1–2) (2013), 58–67.Google Scholar
Brzdęk, J., ‘Note on stability of the Cauchy equation—an answer to a problem of Th. M. Rassias’, Carpathian J. Math. 30(1) (2014), 47–54.Google Scholar
Brzdęk, J., ‘A hyperstability result for the Cauchy equation’, Bull. Aust. Math. Soc. 89(1) (2014), 33–40.Google Scholar
Brzdęk, J. and Ciepliński, K., ‘On a fixed point theorem in 2-Banach spaces and some of its applications’, Acta Math. Sci. Ser. B 38(2) (2018), 377–390.Google Scholar
Brzdęk, J., Ciepliński, K. and Leśniak, Z., ‘On Ulam’s type stability of the linear equation and related issues’, Discrete Dyn. Nat. Soc. 2014 (2014), Article ID 536791.Google Scholar
Brzdęk, J., Fechner, W., Moslehian, M. S. and Sikorska, J., ‘Recent developments of the conditional stability of the homomorphism equation’, Banach J. Math. Anal. 9(3) (2015), 278–326.Google Scholar
Brzdęk, J., Popa, D., Raşa, I. and Xu, B., Ulam Stability of Operators (Academic Press, Elsevier, Oxford, 2018).Google Scholar
Cho, Y. J., Park, C. and Eshaghi Gordji, M., ‘Approximate additive and quadratic mappings in 2-Banach spaces and related topics’, Int. J. Nonlinear Anal. Appl. 3(2) (2012), 75–81.Google Scholar
Chung, S. C. and Park, W.-G., ‘Hyers–Ulam stability of functional equations in 2-Banach spaces’, Int. J. Math. Anal. (Ruse) 6(17–20) (2012), 951–961.Google Scholar
Ciepliński, K., ‘Approximate multi-additive mappings in 2-Banach spaces’, Bull. Iranian Math. Soc. 41(3) (2015), 785–792.Google Scholar
Ciepliński, K. and Surowczyk, A., ‘On the Hyers–Ulam stability of an equation characterizing multi-quadratic mappings’, Acta Math. Sci. Ser. B 35(3) (2015), 690–702.Google Scholar
Ciepliński, K. and Xu, T. Z., ‘Approximate multi-Jensen and multi-quadratic mappings in 2-Banach spaces’, Carpathian J. Math. 29(2) (2013), 159–166.Google Scholar
Freese, R. W. and Cho, Y. J., Geometry of Linear 2-normed Spaces (Nova Science, Hauppauge, NY, 2001).Google Scholar
Gähler, S., ‘Lineare 2-normierte Räume’, Math. Nachr. 28(1–2) (1964), 1–43.Google Scholar
Gao, J., ‘On the stability of the linear mapping in 2-normed spaces’, Nonlinear Funct. Anal. Appl. 14(5) (2009), 801–807.Google Scholar
Hyers, D. H., ‘On the stability of the linear functional equation’, Proc. Natl. Acad. Sci. USA 27 (1941), 222–224.Google Scholar
Hyers, D. H., Isac, G. and Rassias, Th. M., Stability of Functional Equations in Several Variables (Birkhäuser, Boston, MA, 1998).Google Scholar
Jung, S.-M., Hyers–Ulam–Rassias Stability of Functional Equations in Nonlinear Analysis (Springer, New York, 2011).Google Scholar
Jung, S.-M., Popa, D. and Rassias, Th. M., ‘On the stability of the linear functional equation in a single variable on complete metric groups’, J. Global Optim. 59(1) (2014), 165–171.Google Scholar
Jung, S.-M., Rassias, Th. M. and Mortici, C., ‘On a functional equation of trigonometric type’, Appl. Math. Comput. 252 (2015), 294–303.Google Scholar
Moszner, Z., ‘Stability has many names’, Aequationes Math. 90(5) (2016), 983–999.Google Scholar
Park, W. G., ‘Approximate additive mappings in 2-Banach spaces and related topics’, J. Math. Anal. 376(1) (2011), 193–202.Google Scholar
Piszczek, M., ‘Remark on hyperstability of the general linear equation’, Aequationes Math. 88(1–2) (2013), 163–168.Google Scholar
Piszczek, M., ‘Hyperstability of the general linear functional equation’, Bull. Korean Math. Soc. 52(6) (2015), 1827–1838.Google Scholar
Zhang, D., ‘On hyperstability of generalised linear functional equations in several variables’, Bull. Aust. Math. Soc. 92(2) (2015), 259–267.Google Scholar