Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-03T03:41:25.875Z Has data issue: false hasContentIssue false
  • English
  • Français

On analytic functions with reference to the Bernardi integral operator

Published online by Cambridge University Press:  17 April 2009

G. Lakshma Reddy  and
K.S. Padmanabhan
G. Lakshma Reddy
Affiliation:
The Ramanujan Institute for Advanced Study in Mathematics, University of Madras, Madras 600 005, India.
K.S. Padmanabhan
Affiliation:
The Ramanujan Institute for Advanced Study in Mathematics, University of Madras, Madras 600 005, India.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Bernardi has proved that if f if starlike univalent in the uni disc E, then so is the function g given by

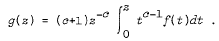
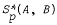In the first part of the paper, we extend Bernardi's theorem to a certain class of p-valent starlike functions in E. We prove that if 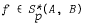then g, defined by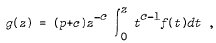

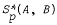also belongs to . In the second part of the paper we examine the converse problem for functions with negative coefficients, satisfying certain conditions.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 25 , Issue 3 , June 1982 , pp. 387 - 396
Copyright
Copyright © Australian Mathematical Society 1982

References

[1]Bernardi, S.D., “Convex and starlike univalent functions”, Trans. Amer. Math. Soc. 135 (1969), 429–446.Google Scholar
[2]Libera, R.J., “Some classes of regular univalent functions”, Proc. Amer. Math. Soc. 16 (1965), 755–758.CrossRefGoogle Scholar
[3]Silverman, Herb, “Extreme points of univalent functions with two fixed points”, Trans. Amer. Math. Soc. 219 (1976), 387–395.Google Scholar