Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T05:14:50.280Z Has data issue: false hasContentIssue false
  • English
  • Français

ON ALGEBRA ISOMORPHISMS BETWEEN p-BANACH BEURLING ALGEBRAS

Part of: Abstract harmonic analysis

Published online by Cambridge University Press:  11 January 2021

PRAKASH A. DABHI Open the ORCID record for PRAKASH A. DABHI [Opens in a new window]  and
DARSHANA B. LIKHADA Open the ORCID record for DARSHANA B. LIKHADA [Opens in a new window]
PRAKASH A. DABHI
Affiliation:
Department of Mathematics, Institute of Infrastructure Technology Research and Management (IITRAM), Ahmedabad380026, Gujarat, India e-mail: [email protected], [email protected]
DARSHANA B. LIKHADA*
Affiliation:
Department of Mathematics, Sardar Patel University, Vallabh Vidyanagar388120, Gujarat, India Current address: Indian Institute of Teacher Education (IITE), Gandhinagar382016, Gujarat, India e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 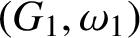$(G_1,\omega _1)$ and 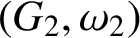$(G_2,\omega _2)$ be weighted discrete groups and 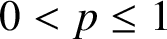$0<p\leq 1$ . We characterise biseparating bicontinuous algebra isomorphisms on the p-Banach algebra 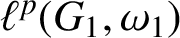$\ell ^p(G_1,\omega _1)$ . We also characterise bipositive and isometric algebra isomorphisms between the p-Banach algebras $\ell ^p(G_1,\omega _1)$ and 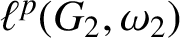$\ell ^p(G_2,\omega _2)$ and isometric algebra isomorphisms between 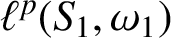$\ell ^p(S_1,\omega _1)$ and 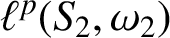$\ell ^p(S_2,\omega _2)$ , where 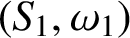$(S_1,\omega _1)$ and $(S_2,\omega _2)$ are weighted discrete semigroups.

Keywords

algebra isomorphismbiseparating and isometric isomorphismsp-Banach algebraweighted Lp algebras for 0 < p ≤ 1

MSC classification

Primary: 43A22: Homomorphisms and multipliers of function spaces on groups, semigroups, etc.
Secondary: 43A20: $L^1$-algebras on groups, semigroups, etc.
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 2 , October 2021 , pp. 308 - 319
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author is grateful to SERB, India for the MATRICS grant (MTR/2019/000162). The second author is thankful to UGC-INDIA for National Fellowship for OBC candidates (F./2016-17/NFO-2015-17-OBC-GUJ-46377/SA-III).

References

Aliprantis, C. D. and Burkinshaw, O., Positive Operators, Pure and Applied Mathematics, 119 (Academic Press, Orlando, FL, 1985).Google Scholar
Bhatt, S. J., Dabhi, P. A. and Dedania, H. V., ‘Beurling algebra analogues of theorems of Wiener–Lévy–Żelazko and Żelazko’, Studia Math. 195(3) (2009), 219–225.CrossRefGoogle Scholar
Dunford, N. and Schwartz, J., Linear Operators. Part I: General Topology (Interscience Publishers, New York, 1957).Google Scholar
Edwards, R. E., ‘Bipositive and isometric isomorphism of some convolution algebras’, Canad. J. Math. 17 (1965), 839–846.CrossRefGoogle Scholar
Ghahramani, F. and Zadeh, S., ‘Bipositive isomorphims of Beurling algebras’, Canad. J. Math. 1 (2017), 3–20.CrossRefGoogle Scholar
Grabiner, S., ‘Weighted shifts and Banach algebras of power series’, Amer. J. Math. 97(1) (1975), 16–42.CrossRefGoogle Scholar
Kalton, N. J. and Wood, G. V., ‘Homomorphisms of group algebras with norm less than $\sqrt{2}$ ’, Pacific J. Math. 62 (1976), 439–460.CrossRefGoogle Scholar
Kawada, Y., ‘On the group ring of a topological group’, Math. Jpn. 1 (1948), 1–5.Google Scholar
Kuznetsova, Y. and Zadeh, S., ‘On isomorphisms between weighted ${L}^p$ -algebras’, Canad. Math. Bull., published online (30 October 2020), 14 pages.CrossRefGoogle Scholar
Lamperti, J., ‘On the isometries of certain function-spaces’, Pacific J. Math. 8(3) (1958), 459–466.CrossRefGoogle Scholar
Larsen, R., An Introduction to the Theory of Multipliers (Springer, Berlin, 1971).CrossRefGoogle Scholar
Loomis, L., An Introduction to Abstract Harmonic Analysis (Van Nostrand, New York, 1953).Google Scholar
Meyer-Nieberg, P., Banach Lattices (Springer, Berlin, 1991).CrossRefGoogle Scholar
Parrott, S. K., ‘Isometric multipliers’, Pacific J. Math. 25 (1) (1968), 159–166.CrossRefGoogle Scholar
Sherbert, D., ‘Banach algebras of Lipschitz functions’, Pacific J. Math. 13 (1963), 1387–1399.CrossRefGoogle Scholar
Strichartz, R. S., ‘Isomorphisms of group algebras’, Proc. Amer. Math. Soc. 17 (1966), 858–862.CrossRefGoogle Scholar
Wendel, J. G., ‘On isometric isomorphism of group algebras’, Pacific J. Math. 1 (1951), 305–311.CrossRefGoogle Scholar
Zadeh, S., ‘Isometric isomorphisms of Beurling algebras’, J. Math. Anal. Appl. 438 (2016), 1–13.CrossRefGoogle Scholar
Żelazko, W., Selected Topics in Topological Algebras, Institut for Matematik Lecture Notes Series, 31 (Aarhus Universitet, Aarhus, 1971).Google Scholar