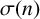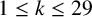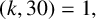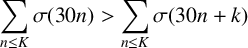Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ding, Yuchen
Pan, Hao
and
Sun, Yu-Chen
2024.
Solutions to some sign change problems on functions involving sums of divisors.
Periodica Mathematica Hungarica,