Published online by Cambridge University Press: 28 November 2018
For a given set 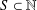 $S\subset \mathbb{N}$,
$S\subset \mathbb{N}$, 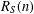 $R_{S}(n)$ is the number of solutions of the equation
$R_{S}(n)$ is the number of solutions of the equation 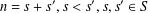 $n=s+s^{\prime },s<s^{\prime },s,s^{\prime }\in S$. Suppose that
$n=s+s^{\prime },s<s^{\prime },s,s^{\prime }\in S$. Suppose that 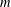 $m$ and
$m$ and  $r$ are integers with
$r$ are integers with 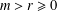 $m>r\geq 0$ and that
$m>r\geq 0$ and that 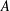 $A$ and
$A$ and 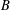 $B$ are sets with
$B$ are sets with 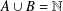 $A\cup B=\mathbb{N}$ and
$A\cup B=\mathbb{N}$ and 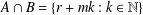 $A\cap B=\{r+mk:k\in \mathbb{N}\}$. We prove that if
$A\cap B=\{r+mk:k\in \mathbb{N}\}$. We prove that if 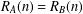 $R_{A}(n)=R_{B}(n)$ for all positive integers
$R_{A}(n)=R_{B}(n)$ for all positive integers  $n$, then there exists an integer
$n$, then there exists an integer 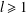 $l\geq 1$ such that
$l\geq 1$ such that 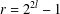 $r=2^{2l}-1$ and
$r=2^{2l}-1$ and 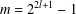 $m=2^{2l+1}-1$. This solves a problem of Chen and Lev [‘Integer sets with identical representation functions’, Integers16 (2016), A36] under the condition
$m=2^{2l+1}-1$. This solves a problem of Chen and Lev [‘Integer sets with identical representation functions’, Integers16 (2016), A36] under the condition 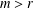 $m>r$.
$m>r$.
The second author was supported by the National Natural Science Foundation of China, Grant No. 11471017. The third author was supported by the National Natural Science Foundation for Youth of China, Grant No. 11501299, the Natural Science Foundation of Jiangsu Province, Grant Nos. BK20150889 and 15KJB110014, and the Startup Foundation for Introducing Talent of NUIST, Grant No. 2014r029.