Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-05T23:10:59.688Z Has data issue: false hasContentIssue false
  • English
  • Français

ON A PARTITION PROBLEM OF FINITE ABELIAN GROUPS

Part of: Sequences and sets Abelian groups

Published online by Cambridge University Press:  29 April 2015

ZHENHUA QU
ZHENHUA QU*
Affiliation:
Department of Mathematics, Shanghai Key Laboratory of PMMP, East China Normal University, 500 Dongchuan Road, Shanghai 200241, PR China email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

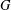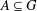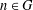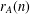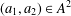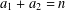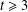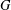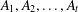Let $G$ be a finite abelian group and $A\subseteq G$. For $n\in G$, denote by $r_{A}(n)$ the number of ordered pairs $(a_{1},a_{2})\in A^{2}$ such that $a_{1}+a_{2}=n$. Among other things, we prove that for any odd number $t\geq 3$, it is not possible to partition $G$ into $t$ disjoint sets $A_{1},A_{2},\dots ,A_{t}$ with 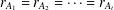$r_{A_{1}}=r_{A_{2}}=\cdots =r_{A_{t}}$.

Keywords

representation functionpartitionfinite abelian group

MSC classification

Primary: 11B34: Representation functions
Secondary: 20K01: Finite abelian groups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 92 , Issue 1 , August 2015 , pp. 24 - 31
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Kiss, S. Z., Rozgonyi, E. and Sándor, C., ‘Groups, partitions and representation functions’, Publ. Math. Debrecen 85(3–4) (2014), 425–433.CrossRefGoogle Scholar
Kiss, S. Z., Rozgonyi, E. and Sándor, C., ‘Sets with almost coinciding representation functions’, Bull. Aust. Math. Soc. 89 (2014), 97–111.CrossRefGoogle Scholar
Lev, V. F., ‘Reconstructing integer sets from their representation functions’, Electron. J. Combin. 11 (2004), R78.CrossRefGoogle Scholar
Nathanson, M. B., ‘Representation functions of sequences in additive number theory’, Proc. Amer. Math. Soc. 72(1) (1978), 16–20.CrossRefGoogle Scholar
Nathanson, M. B., ‘Inverse problems for representation functions in additive number theory’, in: Surveys in Number Theory (ed. Alladi, K.) (Springer, New York, 2008), 89–117.Google Scholar
Sándor, C., ‘Partitions of natural numbers and their representation functions’, Integers 4 (2004), A18.Google Scholar
Sárközy, A. and Sós, V. T., ‘On additive representation functions’, in: The Mathematics of Paul Erdős I (eds. Graham, R. et al. ) (Springer, Berlin, 1997), 129–150.Google Scholar
Tang, M., ‘Partitions of the set of natural numbers and their representation functions’, Discrete Math. 308 (2008), 2614–2616.CrossRefGoogle Scholar