Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
WU, ZHAOJUN
and
SUN, DAOCHUN
2008.
ON T DIRECTION OF ALGEBROID FUNCTION DEALING WITH MULTIPLE VALUES.
Bulletin of the Australian Mathematical Society,
Vol. 78,
Issue. 1,
p.
147.
Xuan, Zu-Xing
2008.
On the existence of T-direction of algebroid functions: A problem of J.H. Zheng.
Journal of Mathematical Analysis and Applications,
Vol. 341,
Issue. 1,
p.
540.
Wu, Zhaojun
and
Sun, Daochun
2009.
On a new singular direction of quasimeromorphic mappings.
Acta Mathematica Scientia,
Vol. 29,
Issue. 5,
p.
1453.
Zheng, Jianhua
2010.
Value Distribution of Meromorphic Functions.
p.
123.
Zheng, J.-H.
2011.
On value distribution of meromorphic functions with respect to arguments I.
Complex Variables and Elliptic Equations,
Vol. 56,
Issue. 1-4,
p.
271.
Zhang, Hongshen
2012.
OnTpoint of algebroid functions in |z| < 1.
Complex Variables and Elliptic Equations,
Vol. 57,
Issue. 9,
p.
929.
Yinying, Kong
2012.
Borel radius and T-Radius of the algebroidal function in the unit disc.
Acta Mathematica Scientia,
Vol. 32,
Issue. 5,
p.
1805.


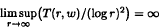 , there exists a
, there exists a 