In his work on a proof of Grushko's theorem by groupoid methods, Philip Higgins proved the following subgroup theorem.

Theorem. Suppose that θ:G → B is a surjective map of groups, where G and B are free products 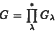and 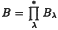, and where θ(Gλ) = Bλ for each λ. Let H be a subgroup of G with the property that the restriction of θ to H is surjective. Then there is a free decomposition 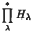of H with θ(Hλ) = Bλ for each λ.

As Higgins has noted, there is a common strategy in the proff of this theorem and in the groupoid proofs of Kurosh and Neilsen-Schreier subgroup theorems. Higgins conjectured the existence of a common generalisation of his theorem and the Kurosh theorem, proposed a plausible statement for such a result, and hinted that the common strategy of these proofs might be extended to give a proof of the conjecture. Examined at more detailed level, however, the common strategy used in the proofs of the Kurosh theorem and Higgin's theorem is seen to diverge into two strads. In this paper, it is shown that the construction entailed in these divergent approaches are in genera; incompatible. Thus any proof of Higgin's conjecture must require substantially different techniques. In particular, the proof of a theorem by Ordman that purports to affirm the conjecture is incorrect, and the approach used in his argument cannot yield a valid proof.