Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T02:23:33.337Z Has data issue: false hasContentIssue false
  • English
  • Français

On 3-dimensional contact slant submanifolds in Sasakian space forms

Published online by Cambridge University Press:  17 April 2009

Ion Mihai  and
Yoshihiko Tazawa
Ion Mihai
Affiliation:
Faculty of Mathematics, Str. Academiei 14, 70109 Bucharest, Romania, e-mail: [email protected]
Yoshihiko Tazawa
Affiliation:
School of Information Environment, Tokyo Denki University, Inzai, Chiba Prefecture 270-1382, Japan, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recently, B.-Y. Chen obtained an inequality for slant surfaces in complex space forms. Further, B.-Y. Chen and one of the present authors proved the non-minimality of proper slant surfaces in non-flat complex space forms. In the present paper, we investigate 3-dimensional proper contact slant submanifolds in Sasakian space forms. A sharp inequality is obtained between the scalar curvature (intrinsic invariant) and the main extrinsic invariant, namely the squared mean curvature.

It is also shown that a 3-dimensional contact slant submanifold M of a Sasakian space form 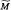(c), with c ≠ 1, cannot be minimal.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 68 , Issue 2 , October 2003 , pp. 275 - 283
Copyright
Copyright © Australian Mathematical Society 2003

References

[1]Blair, D.E., Contact manifolds in Riemannian geometry, Lecture Notes in Math. 509 (Springer-Verlag, Berlin, 1976).CrossRefGoogle Scholar
[2]Cabrerizo, J., Carriazo, A., Fernandez, L.M. and Fernandez, M., ‘Slant submanifolds in Sasakian manifolds’, Glasgow Math. J. 42 (2000), 125–138.CrossRefGoogle Scholar
[3]Chen, B.-Y., ‘On slant surfaces’, Taiwanese J. Math. 3 (1999), 163–179.CrossRefGoogle Scholar
[4]Chen, B.-Y. and Tazawa, Y., ‘Slant submanifolds of complex projective and complex hyperbolic spaces’, Glasgow Math. J. 42 (2000), 439–454.CrossRefGoogle Scholar
[5]De Smet, P.J., Dillen, F., Verstraelen, L. and Vrancken, L., ‘A pointwise inequality in submanifold theory’, Arch. Math. (Brno) 35 (1999), 115–128.Google Scholar
[6]Wintgen, P., ‘Sur l'inégalité de Chen-Willmore’, C.R. Acad. Sci. Paris 288 (1979), 993–995.Google Scholar
[7]Yano, K. and Kon, M., Anti-invariant submanifolds, Lecture Notes in Pure and Applied Mathematics (Marcel Dekker, New York, Basel, 1976).Google Scholar
[8]Yano, K. and Kon, M., Structures on manifolds, Series in Pure Mathematics 3 (World Scientific, Singapore, 1984).Google Scholar