Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T19:38:19.236Z Has data issue: false hasContentIssue false
  • English
  • Français

ODD MULTIPERFECT NUMBERS

Part of: Elementary number theory

Published online by Cambridge University Press:  06 November 2012

SHI-CHAO CHEN  and
HAO LUO
SHI-CHAO CHEN*
Affiliation:
Institute of Contemporary Mathematics,Department of Mathematics and Information Sciences, Henan University, Kaifeng 475001, PR China (email: [email protected])
HAO LUO
Affiliation:
Institute of Contemporary Mathematics,Department of Mathematics and Information Sciences, Henan University, Kaifeng 475001, PR China (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A natural number $n$ is called multiperfect or 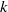$k$-perfect for integer 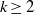$k\ge 2$ if 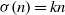$\sigma (n)=kn$, where $\sigma (n)$ is the sum of the positive divisors of $n$. In this paper, we establish a theorem on odd multiperfect numbers analogous to Euler’s theorem on odd perfect numbers. We describe the divisibility of the Euler part of odd multiperfect numbers and characterise the forms of odd perfect numbers 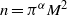$n=\pi ^\alpha M^2$ such that 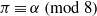$\pi \equiv \alpha ~({\rm mod}~8)$, where 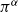$\pi ^\alpha $ is the Euler factor of $n$. We also present some examples to show the nonexistence of odd perfect numbers of certain forms.

Keywords

odd multiperfect numbersEuler partnonexistence

MSC classification

Secondary: 11A05: Multiplicative structure; Euclidean algorithm; greatest common divisors
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 1 , August 2013 , pp. 56 - 63
Copyright
Copyright © 2012 Australian Mathematical Publishing Association Inc. 

References

[1]Broughan, K. & Zhou, Q., ‘Odd multiperfect numbers of abundancy 4’, J. Number Theory 128 (2008), 1566–1575.CrossRefGoogle Scholar
[2]Cohen, G. L. & Williams, R. J., ‘Extensions of some results concerning odd perfect numbers’, Fibonacci Quart. 23 (1985), 70–76.Google Scholar
[3]Ewell, J. A., ‘On the multiplicative structure of odd perfect numbers’, J. Number Theory 12 (1980), 339–342.CrossRefGoogle Scholar
[4]Flammenkamp, A., ‘The multiply perfect numbers page’,http://wwwhomes.uni-bielefeld.de/achim/mpn.html.Google Scholar
[5]Hagis, P. & McDaniel, W. L., ‘A new result concerning the structure of odd perfect numbers’, Proc. Amer. Math. Soc. 32 (1972), 13–15.CrossRefGoogle Scholar
[6]Kanold, H.-J., ‘Untersuchungen über ungerade vollkommene Zahlen’, J. reine angew. Math. 183 (1941), 98–109.CrossRefGoogle Scholar
[7]McDaniel, W. L., ‘The nonexistence of odd perfect numbers of a certain form’, Arch. Math. 21 (1970), 52–53.CrossRefGoogle Scholar
[8]McDaniel, W. L. & Hagis, P., ‘Some results concerning the nonexistence of odd perfect numbers of the form $p^\alpha M^{2\beta }$’, Fibonacci Quart. 13 (1975), 25–28.Google Scholar
[9]Nagell, T., Introduction to Number Theory (AMS Chelsea Publishing, Providence, RI, 1981).Google Scholar
[10]Starni, P., ‘On the Euler’s factor of an odd perfect number’, J. Number Theory 37 (1991), 366–369.CrossRefGoogle Scholar
[11]Starni, P., ‘On some properties of the Euler’s factor of certain odd perfect numbers’, J. Number Theory 116 (2006), 483–486.CrossRefGoogle Scholar