Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wall, G.E.
1980.
Conjugacy classes in projective and special linear groups.
Bulletin of the Australian Mathematical Society,
Vol. 22,
Issue. 3,
p.
339.
Zalesskii, A. E.
1985.
Linear groups.
Journal of Soviet Mathematics,
Vol. 31,
Issue. 3,
p.
2974.
Higgs, R. J.
1988.
Groups with two projective characters.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 103,
Issue. 1,
p.
5.
Kondrat'ev, A. S.
Makhnev, A. A.
and
Starostin, A. I.
1989.
Finite groups.
Journal of Soviet Mathematics,
Vol. 44,
Issue. 3,
p.
237.
Fleischmann, Peter
and
Janiszczak, Ingo
1996.
On the computation of conjugacy classes of Chevalley groups.
Applicable Algebra in Engineering, Communication and Computing,
Vol. 7,
Issue. 3,
p.
221.
Fleischmann, Peter
1997.
Polynomial identities for orbit numbers of general linear and unitary groups over finite fields.
Linear Algebra and its Applications,
Vol. 253,
Issue. 1-3,
p.
341.
Liebeck, Martin W.
and
Pyber, László
1997.
Upper Bounds for the Number of Conjugacy Classes of a Finite Group.
Journal of Algebra,
Vol. 198,
Issue. 2,
p.
538.
Kohl, Stefan
2002.
COUNTING THE ORBITS ON FINITE SIMPLE GROUPS UNDER THE ACTION OF THE AUTOMORPHISM GROUP – SUZUKI GROUPS VS. LINEAR GROUPS.
Communications in Algebra,
Vol. 30,
Issue. 7,
p.
3515.
Kohl, Stefan
2004.
Classifying Finite Simple Groups with Respect to the Number of Orbits Under the Action of the Automorphism Group.
Communications in Algebra,
Vol. 32,
Issue. 12,
p.
4785.
Guralnick, Robert M.
and
Tiep, Pham Huu
2005.
The non-coprime k(GV) problem.
Journal of Algebra,
Vol. 293,
Issue. 1,
p.
185.
Harada, Shinya
and
Moon, Hyunsuk
2008.
On zeta functions of modular representations of a discrete group.
Journal of Algebra,
Vol. 319,
Issue. 11,
p.
4456.
Gill, Nick
and
Singh, Anupam
2011.
Real and strongly real classes in SL n (q).
Journal of Group Theory,
Vol. 14,
Issue. 3,
Gill, Nick
and
Singh, Anupam
2011.
Real and strongly real classes in PGL n (q) and quasi-simple covers of PSL n (q).
Journal of Group Theory,
Vol. 14,
Issue. 3,
Sim, Hyo-Seob
and
Song, Hyun-Jong
2014.
REVISIT TO CONNECTED ALEXANDER QUANDLES OF SMALL ORDERS VIA FIXED POINT FREE AUTOMORPHISMS OF FINITE ABELIAN GROUPS.
East Asian mathematical journal,
Vol. 30,
Issue. 3,
p.
293.
Fantino, Fernando
2014.
Conjugacy Classes ofP-Cycles of Type D in Alternating Groups.
Communications in Algebra,
Vol. 42,
Issue. 10,
p.
4426.
Schaeffer Fry, Amanda A.
and
Vinroot, C. Ryan
2016.
Real classes of finite special unitary groups.
Journal of Group Theory,
Vol. 19,
Issue. 5,
p.
735.
Merca, Mircea
2017.
Lambert series and conjugacy classes in GL
.
Discrete Mathematics,
Vol. 340,
Issue. 9,
p.
2223.
Merca, Mircea
2018.
Binomial transforms and integer partitions into parts of k different magnitudes.
The Ramanujan Journal,
Vol. 46,
Issue. 3,
p.
765.
Bhunia, Sushil
and
Singh, Anupam
2019.
Conjugacy classes of centralizers in unitary groups.
Journal of Group Theory,
Vol. 22,
Issue. 2,
p.
231.
AMPARO, ELENA
and
VINROOT, C. RYAN
2020.
ON THE NUMBER OF REAL CLASSES IN THE FINITE PROJECTIVE LINEAR AND UNITARY GROUPS.
Glasgow Mathematical Journal,
Vol. 62,
Issue. 1,
p.
93.


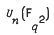 ;
; 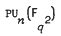 ,
, 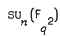 , and more generally
, and more generally 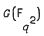 where
where 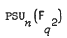 .
.