Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T03:13:04.618Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON WIELANDT’S THEOREM

Part of: Representation theory of groups

Published online by Cambridge University Press:  09 February 2022

HANGYANG MENG Open the ORCID record for HANGYANG MENG [Opens in a new window]  and
XIUYUN GUO Open the ORCID record for XIUYUN GUO [Opens in a new window]
HANGYANG MENG*
Affiliation:
Department of Mathematics, Shanghai University, Shanghai 200444, PR China
XIUYUN GUO
Affiliation:
Department of Mathematics, Shanghai University, Shanghai 200444, PR China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

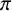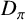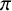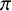Let $\pi $ be a set of primes. We say that a group G satisfies $D_{\pi }$ if G possesses a Hall $\pi $ -subgroup H and every $\pi $ -subgroup of G is contained in a conjugate of H. We give a new 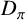$D_{\pi }$ -criterion following Wielandt’s idea, which is a generalisation of Wielandt’s and Rusakov’s results.

Keywords

Hall π-subgroupcyclic Sylow subgroupp-nilpotent

MSC classification

Primary: 20D20: Sylow subgroups, Sylow properties, $pi$-groups, $pi$-structure
Secondary: 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 106 , Issue 2 , October 2022 , pp. 310 - 314
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author’s research was sponsored by the Young Scientists Fund of the NSFC (12001359) and the Shanghai Sailing Program (20YF1413400). The second author’s research was partially supported by the National Natural Science Foundation of China (12171302).

References

Guo, W., Revin, D. O. and Vdovin, E. P., ‘Confirmation for Wielandt’s conjecture’, J. Algebra 434 (2015), 193–206.CrossRefGoogle Scholar
Hall, P., ‘Theorems like Sylow’s’, Proc. Lond. Math. Soc. (3) 6 (1956), 286–304.CrossRefGoogle Scholar
Huppert, B., Endliche Gruppen I , Grundlehren der mathematischen Wissenschaften, 134 (Springer, Berlin, 1967).Google Scholar
Rusakov, S. A., ‘Analogues of Sylow’s theorem on inclusion of subgroups’, Dokl. Akad. Nauk BSSR 5 (1961), 139–141.Google Scholar
Wielandt, H., ‘Zum Satz von Sylow’, Math. Z. 60 (1954), 407–408.CrossRefGoogle Scholar
Wielandt, H., ‘Zum Satz von Sylow. II’, Math. Z. 71 (1959), 461–462.CrossRefGoogle Scholar