No CrossRef data available.
Article contents
A note on tensor products of reflexive algebras
Published online by Cambridge University Press: 17 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this short note, we obtain a concrete description of rank-one operators in Alg(ℒ1 ⊗…⊗ ℒn). Based on this characterisation, we give a simple proof of the tensor product formula:
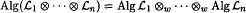if Alg(ℒ1 ⊗…⊗ ℒn) is weakly generated by rank-one operators in itself and ℒi(i = 1,…,n) are subspace lattices.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 2002
References
[1]Gilfeather, F., Hopenwasser, A. and Larson, D., ‘Reflexive algebras with finite width latices: tensor products, cohomology, compact perturbation’, J. Funct. Anal. 55 (1984), 176–199.Google Scholar
[2]Hopenwasser, A. and Kraus, J., ‘Tensor products of reflexive algebras II’, J. London Math. Soc. 2 28 (1983), 359–362.Google Scholar
[3]Hopenwasser, A., Laurie, C. and Moore, R., ‘Reflexive algebras with completely distributive subspace lattices’, J. Operator Theory 11 (1984), 91–108.Google Scholar
[4]Kraus, J., ‘Tensor products of reflexive algebras’, J. London Math. Soc. 2 28 (1983), 350–358.CrossRefGoogle Scholar
[5]Laurie, C. and Longstaff, W.E., ‘A note on rank-one operators in reflexive algebras’, Proc. Amer. Math. Soc. 89 (1983), 293–297.CrossRefGoogle Scholar
[6]Longstaff, W.E., ‘Strongly reflexive lattices’, J. London Math. Soc. 2 11 (1975), 491–498.Google Scholar
You have
Access