No CrossRef data available.
Article contents
A NOTE ON SUBNORMAL SUBGROUPS IN DIVISION RINGS CONTAINING SOLVABLE SUBGROUPS
Part of:
Rings and algebras arising under various constructions
Division rings and semisimple Artin rings
Structure and classification of infinite or finite groups
Published online by Cambridge University Press: 11 January 2023
Abstract
Let D be a division ring and N be a subnormal subgroup of the multiplicative group 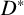 $D^*$. We show that if N contains a nonabelian solvable subgroup, then N contains a nonabelian free subgroup.
$D^*$. We show that if N contains a nonabelian solvable subgroup, then N contains a nonabelian free subgroup.
MSC classification
Primary:
16K20: Finite-dimensional
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 108 , Issue 3 , December 2023 , pp. 422 - 427
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The first author is funded by Vietnam National University Ho Chi Minh City (VNUHCM) under grant number T2022-18-03.
References
Bell, J. P. and Gonçalves, J., ‘On free subgroups in division rings’, Proc. Amer. Math. Soc. 148 (2020), 1953–1962.10.1090/proc/14888CrossRefGoogle Scholar
Bien, M. H. and Hai, B. X., ‘On subnormal subgroups in division rings containing a non-abelian solvable subgroup’, Bull. Math. Soc. Sci. Math. Roumanie (N.S.) 63(111)(2) (2020), 151–162.Google Scholar
Danh, L. Q. and Khanh, H. V., ‘Locally solvable subnormal and quasinormal subgroups in division rings’, Hiroshima Math. J. 51 (2021), 267–274.Google Scholar
Gonçalves, J. Z., ‘Free groups in subnormal subgroups and the residual nilpotence of the group of units of group rings’, Canad. Math. Bull. 27 (1984), 365–370.10.4153/CMB-1984-055-6CrossRefGoogle Scholar
Gonçalves, J. Z. and Mandel, A., ‘Are there free groups in division rings?’, Israel J. Math. 53 (1986), 69–80.10.1007/BF02772670CrossRefGoogle Scholar
Goodearl, K. R. and Warfield, R. B. Jr, An Introduction to Noncommutative Noetherian Rings, London Mathematical Society Student Texts, 61 (Cambridge University Press, Cambridge, 2004).10.1017/CBO9780511841699CrossRefGoogle Scholar
Hai, B. X. and Thin, N. V., ‘On locally nilpotent subgroups of
 ${\mathrm{GL}}_1(D)$
’, Comm. Algebra 37(2) (2009), 712–718.10.1080/00927870802255287CrossRefGoogle Scholar
${\mathrm{GL}}_1(D)$
’, Comm. Algebra 37(2) (2009), 712–718.10.1080/00927870802255287CrossRefGoogle Scholar
Hai, B. X. and Thin, N. V., ‘On subnormal subgroups in general skew linear groups’, Vestnik St. Petersburg Univ. Math. 46 (2013), 43–48.10.3103/S1063454113010020CrossRefGoogle Scholar
Lam, T. Y., A First Course in Noncommutative Rings, Graduate Texts in Mathematics, 131 (Springer, Berlin, 2001).10.1007/978-1-4419-8616-0CrossRefGoogle Scholar
Lichtman, A. I., ‘On subgroups of the multiplicative group of skew fields’, Proc. Amer. Math. Soc. 63(1) (1977), 15–16.10.1090/S0002-9939-1977-0447432-0CrossRefGoogle Scholar
Lichtman, A. I., ‘Free subgroups of normal subgroups of the multiplicative group of skew fields’, Proc. Amer. Math. Soc. 7 (1978), 174–178.10.1090/S0002-9939-1978-0480623-2CrossRefGoogle Scholar
Ore, O., ‘Theory of non-commutative polynomials’, Ann. of Math. (2) 34(3) (1933), 480–508.10.2307/1968173CrossRefGoogle Scholar
Tits, J., ‘Free subgroups in linear groups’, J. Algebra 20 (1972), 250–270.10.1016/0021-8693(72)90058-0CrossRefGoogle Scholar



