Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T00:04:39.296Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON RAMSEY NUMBERS FOR FANS

Part of: Graph theory Extremal combinatorics

Published online by Cambridge University Press:  13 May 2015

YANBO ZHANG ,
HAJO BROERSMA  and
YAOJUN CHEN
YANBO ZHANG
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, PR China Faculty of Electrical Engineering, Mathematics and Computer Science, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
HAJO BROERSMA
Affiliation:
Faculty of Electrical Engineering, Mathematics and Computer Science, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
YAOJUN CHEN*
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For two given graphs 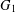$G_{1}$ and 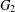$G_{2}$, the Ramsey number 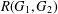$R(G_{1},G_{2})$ is the smallest integer 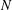$N$ such that, for any graph 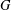$G$ of order 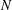$N$, either 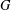$G$ contains 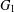$G_{1}$ as a subgraph or the complement of 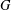$G$ contains 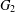$G_{2}$ as a subgraph. A fan 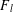$F_{l}$ is 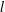$l$ triangles sharing exactly one vertex. In this note, it is shown that 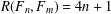$R(F_{n},F_{m})=4n+1$ for 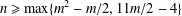$n\geq \max \{m^{2}-m/2,11m/2-4\}$.

Keywords

Ramsey numberfangoodness

MSC classification

Primary: 05D10: Ramsey theory
Secondary: 05C70: Factorization, matching, partitioning, covering and packing
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 92 , Issue 1 , August 2015 , pp. 19 - 23
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Burr, S. A., ‘Ramsey numbers involving graphs with long suspended paths’, J. Lond. Math. Soc. (2) 24 (1981), 405–413.CrossRefGoogle Scholar
Chvátal, V. and Harary, F., ‘Generalized Ramsey theory for graphs, III. Small off-diagonal numbers’, Pacific J. Math. 41 (1972), 335–345.CrossRefGoogle Scholar
Hall, P., ‘On representatives of subsets’, J. Lond. Math. Soc. (2) 10 (1935), 26–30.CrossRefGoogle Scholar
Li, Y. S. and Rousseau, C. C., ‘Fan-complete graph Ramsey numbers’, J. Graph Theory 23 (1996), 413–420.3.0.CO;2-D>CrossRefGoogle Scholar
Lin, Q. Z. and Li, Y. S., ‘On Ramsey numbers of fans’, Discrete Appl. Math. 157 (2009), 191–194.CrossRefGoogle Scholar
Lin, Q. Z., Li, Y. S. and Dong, L., ‘Ramsey goodness and generalized stars’, European J. Combin. 31 (2010), 1228–1234.CrossRefGoogle Scholar