Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T02:36:13.265Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON PARACOMPACT p-SPACES AND THE MONOTONE D-PROPERTY

Part of: Maps and general types of spaces defined by maps Special properties Fairly general properties

Published online by Cambridge University Press:  07 February 2011

YIN-ZHU GAO  and
WEI-XUE SHI
YIN-ZHU GAO*
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, PR China (email: [email protected])
WEI-XUE SHI
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, PR China (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For any generalized ordered space X with the underlying linearly ordered topological space Xu, let X* be the minimal closed linearly ordered extension of X and 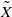be the minimal dense linearly ordered extension of X. The following results are obtained.

  1. (1) The projection mapping π:X*→X, π(〈x,i〉)=x, is closed.

  2. (2) The projection mapping 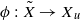, ϕ(〈x,i〉)=x, is closed.

  3. (3) X* is a monotone D-space if and only if X is a monotone D-space.

  4. (4) 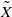is a monotone D-space if and only if Xu is a monotone D-space.

  5. (5) For the Michael line M, 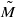is a paracompact p-space, but not continuously Urysohn.

Keywords

paracompactnesscontinuously Urysohncompactnessmonotone Dgeneralized ordered spaces

MSC classification

Secondary: 54C10: Special maps on topological spaces (open, closed, perfect, etc.) 54D20: Noncompact covering properties (paracompact, Lindelöf, etc.) 54D30: Compactness 54F05: Linearly ordered topological spaces, generalized ordered spaces, and partially ordered spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 83 , Issue 3 , June 2011 , pp. 463 - 469
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2011

Footnotes

This project is supported by NSFC (No. 10971092).

References

[1]Bennett, H. R. and Lutzer, D. J., ‘Problems in perfect ordered spaces’, in: Open Problems in Topology, (eds. van Mill, J. and Reed, G. M.) (Elsevier Science, Amsterdam, 1990), pp. 231–236.Google Scholar
[2]Bennett, H. R. and Lutzer, D. J., ‘Continuous separating families in ordered spaces and strong base conditions’, Topology Appl. 119 (2002), 305–314.CrossRefGoogle Scholar
[3]Gao, Y.-Z. and Shi, W.-X., ‘The D-property and the Sorgenfrey line’, Bull. Aust. Math. Soc. 80 (2009), 233–236.CrossRefGoogle Scholar
[4]Halbeisen, L. and Hungerbühler, N., ‘On continuously Urysohn and strongly separating spaces’, Topology Appl. 118 (2002), 329–335.CrossRefGoogle Scholar
[5]Miwa, T. and Kemoto, N., ‘Linearly ordered extensions of GO-spaces’, Topology Appl. 54 (1993), 133–140.CrossRefGoogle Scholar
[6]Popvassilev, S. G. and Porter, J. E., ‘Monotonically D-spaces’, Topology Proc. 30 (2006), 355–365.Google Scholar
[7]Shi, W.-X., ‘Perfect GO-spaces which have a perfect linearly ordered extension’, Topology Appl. 81 (1997), 23–33.CrossRefGoogle Scholar
[8]Shi, W.-X. and Gao, Y.-Z., ‘Sorgenfrey line and continuous separating families’, Topology Appl. 142 (2004), 89–94.CrossRefGoogle Scholar
[9]Shi, W.-X., Miwa, T. and Gao, Y.-Z., ‘A perfect GO-space which cannot densely embed in any perfect orderable space’, Topology Appl. 66 (1995), 241–249.Google Scholar
[10]Stepanova, E. N., ‘Extension of continuous functions and metrizability of paracompact p-spaces’, Math. Notes (Mat. Zametki) 53 (1993), 308–314.CrossRefGoogle Scholar
[11]van Douwen, E. K. and Pfeffer, W. F., ‘Some properties of the Sorgenfrey line and related spaces’, Pacific J. Math. 81 (1979), 371–377.CrossRefGoogle Scholar