Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-24T02:10:46.339Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON NORMAL COMPLEMENTS FOR FINITE GROUPS

Part of: Representation theory of groups

Published online by Cambridge University Press:  29 April 2018

NING SU ,
ADOLFO BALLESTER-BOLINCHES Open the ORCID record for ADOLFO BALLESTER-BOLINCHES [Opens in a new window]  and
HANGYANG MENG Open the ORCID record for HANGYANG MENG [Opens in a new window]
NING SU
Affiliation:
Department of Mathematics, Sun Yat-sen University, Guangzhou 510275, China email [email protected]
ADOLFO BALLESTER-BOLINCHES*
Affiliation:
Departament de Matemàtiques, Universitat de València, 46100 Burjassot, València, Spain email [email protected]
HANGYANG MENG
Affiliation:
Departament de Matemàtiques, Universitat de València, 46100 Burjassot, València, Spain email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Assume that 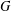$G$ is a finite group and 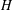$H$ is a 2-nilpotent Sylow tower Hall subgroup of 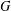$G$ such that if $x$ and 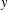$y$ are 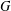$G$-conjugate elements of 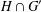$H\cap G^{\prime }$ of prime order or order 4, then $x$ and 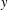$y$ are 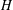$H$-conjugate. We prove that there exists a normal subgroup 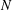$N$ of 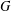$G$ such that 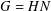$G=HN$ and 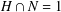$H\cap N=1$.

Keywords

finite groupsconjugationHall subgroupsnormal complements

MSC classification

Primary: 20D20: Sylow subgroups, Sylow properties, $pi$-groups, $pi$-structure
Secondary: 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 1 , August 2018 , pp. 109 - 112
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author is supported by the National Natural Science Foundation of China (no. 11401597). The second and third authors have been supported by the grant MTM2014-54707-C3-1-P from the Ministerio de Economía y Competitividad, Spain, and FEDER, European Union. The second author is also supported by Prometeo/2017/057 of Generalitat (Valencian Community, Spain) and the third author is also supported by the China Scholarship Council, grant no. 201606890006.

References

Ballester-Bolinches, A., Ezquerro, L. M. and Skiba, A. N., ‘On subgroups of hypercentral type of finite groups’, Israel J. Math. 199 (2014), 259–265.Google Scholar
Doerk, K. and Hawkes, T., Finite Soluble Groups, De Gruyter Expositions in Mathematics, 4 (Walter de Gruyter, Berlin–New York, 1992).CrossRefGoogle Scholar
González-Sánchez, J., ‘A p-nilpotency criterion’, Arch. Math. (Basel) 94 (2010), 201–205.Google Scholar
Gorenstein, D., Finite Groups (Chelsea, New York, 1980).Google Scholar
Isaacs, I. M., Character Theory of Finite Groups (Academic Press, New York, 1976).Google Scholar
Rose, J. S., A Course on Group Theory (Cambridge University Press, London–New York–Melbourne, 1978).Google Scholar