Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T11:00:42.643Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on Nk configurations and theorems in projective space

Published online by Cambridge University Press:  17 April 2009

David G. Glynn
David G. Glynn
Affiliation:
School of Mathematical Sciences, University of Adelaide, Adelaide SA 5005, Australia e-mail: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A method of embedding nk configurations into projective space of k–1 dimensions is given. It breaks into the easy problem of finding a rooted spanning tree of the associated Levi graph. Also it is shown how to obtain a “complementary” 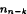“theorem” about projective space (over a field or skew-field F) from any nk theorem over F. Some elementary matroid theory is used, but with an explanation suitable for most people. Various examples are mentioned, including the planar configurations: Fano 73, Pappus 93, Desargues 103 (also in 3d-space), Möbius 84 (in 3d-space), and the resulting 74 in 3d-space, 96 in 5d-space, and 107 in 6d-space. (The Möbius configuration is self-complementary.) There are some nk configurations that are not embeddable in certain projective spaces, and these will be taken to similarly not embeddable configurations by complementation. Finally, there is a list of open questions.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 76 , Issue 1 , August 2007 , pp. 15 - 31
Copyright
Copyright © Australian Mathematical Society 2007

References

[1]Baker, H.F., Principles of geometry I–IV (Cambridge University Press, Cambridge, 1922–1925).Google Scholar
[2]Bokowski, J. and Sturmfels, B., Computational synthetic geometry, Lecture Notes in Math. 1355 (Springer-Verlag, Heidelberg, 1989).Google Scholar
[3]Dembowski, P., Finite geometries (Springer-Verlag, New York, 1968).CrossRefGoogle Scholar
[4]Glynn, D.G., ‘On the anti-Pappian 103 configuration and its construction”, Geom. Dedicata 77 (1999), 71–75.CrossRefGoogle Scholar
[5]Glynn, D.G., ‘On the representation of configurations in projective spaces’, J. Statist. Plann. Inference 86 (2000), 443–456.CrossRefGoogle Scholar
[6]Glynn, D.G., ‘Transformations of codes and geometry related to Veroneseans’, (preprint, see http://internal.maths.adelaide.edu.au/people/rcasse/DavidGlynn/papers.html).Google Scholar
[7]Gropp, H., ‘Configurations and their realization’, Discrete Math. 174 (1997), 137–151.Google Scholar
[8]Grünbaum, B., ‘3-connected configurations (n3) with no Hamiltonian circuit’, Bull. Inst. Combin. Appl. 46 (2006), 15–26.Google Scholar
[9]Hirschfeld, J.W.P. and Thas, J.A., General Galois geometries (Clarendon Press, Oxford, 1991).Google Scholar
[10]Levi, F.W., Finite geometrical systems, (six public lectures by the Hardinge Professor) (University of Calcutta, Calcutta, 1942).Google Scholar
[11]Möbius, A.F., J. f. Math. 3 (1828), 276. Werke 1 (1885), 437–443.Google Scholar
[12]Steinitz, E., ‘Konfigurationen der projektiven Geometrie’, Encyklopädie der Mathematischen Wissenschaften, mit Einschluss ihrer Anwendungen, Vol. 3, Part 1, 1st Half: Geometrie (1910), 481–516.CrossRefGoogle Scholar
[13]Sturmfels, B., ‘Computational algebraic geometry of projective configurations’, J. Symbolic Comput. 11 (1991), 595–618.CrossRefGoogle Scholar
[14]Wallace, W. (1806), See Camb. Phil. Proc., Vol. XXI, 1923, 348.Google Scholar