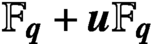 $\mathbb {F}_{\mathbf{\mathit{q}}}\boldsymbol{+}\mathbf{\mathit{u}}\mathbb {F}_{\mathbf{\mathit{q}}}$
$\mathbb {F}_{\mathbf{\mathit{q}}}\boldsymbol{+}\mathbf{\mathit{u}}\mathbb {F}_{\mathbf{\mathit{q}}}$Published online by Cambridge University Press: 14 December 2020
We study the k-Galois linear complementary dual (LCD) codes over the finite chain ring
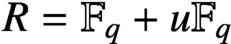 $R=\mathbb {F}_q+u\mathbb {F}_q$
with
$R=\mathbb {F}_q+u\mathbb {F}_q$
with
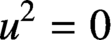 $u^2=0$
, where
$u^2=0$
, where
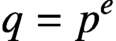 $q=p^e$
and p is a prime number. We give a sufficient condition on the generator matrix for the existence of k-Galois LCD codes over R. Finally, we show that a linear code over R (for
$q=p^e$
and p is a prime number. We give a sufficient condition on the generator matrix for the existence of k-Galois LCD codes over R. Finally, we show that a linear code over R (for
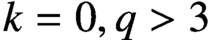 $k=0, q> 3$
) is equivalent to a Euclidean LCD code, and a linear code over R (for
$k=0, q> 3$
) is equivalent to a Euclidean LCD code, and a linear code over R (for
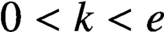 $0<k<e$
,
$0<k<e$
,
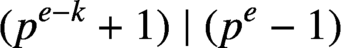 $(p^{e-k}+1)\mid (p^e-1)$
and
$(p^{e-k}+1)\mid (p^e-1)$
and
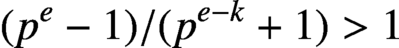 ${(p^e-1)}/{(p^{e-k}+1)}>1$
) is equivalent to a k-Galois LCD code.
${(p^e-1)}/{(p^{e-k}+1)}>1$
) is equivalent to a k-Galois LCD code.
This research is supported by the National Natural Science Foundation of China (12071001, 61672036), the Excellent Youth Foundation of Natural Science Foundation of Anhui Province (1808085J20), the Academic Fund for Outstanding Talents in Universities (gxbjZD03) and the Natural Science Foundation of Anhui Provence (2008085QA04).