Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T02:00:55.058Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON INHOMOGENEOUS DIOPHANTINE APPROXIMATION IN BETA-DYNAMICAL SYSTEM

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Classical measure theory

Published online by Cambridge University Press:  12 September 2014

YUEHUA GE  and
FAN LÜ
YUEHUA GE
Affiliation:
Huazhong University of Science and Technology, Wuhan 430074, PR China email [email protected]
FAN LÜ*
Affiliation:
Huazhong University of Science and Technology, Wuhan 430074, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

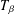We study the distribution of the orbits of real numbers under the beta-transformation $T_{{\it\beta}}$ for any 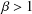${\it\beta}>1$. More precisely, for any real number 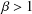${\it\beta}>1$ and a positive function 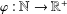${\it\varphi}:\mathbb{N}\rightarrow \mathbb{R}^{+}$, we determine the Lebesgue measure and the Hausdorff dimension of the following set:

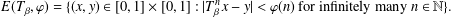$$\begin{eqnarray}E(T_{{\it\beta}},{\it\varphi})=\{(x,y)\in [0,1]\times [0,1]:|T_{{\it\beta}}^{n}x-y|<{\it\varphi}(n)\text{ for infinitely many }n\in \mathbb{N}\}.\end{eqnarray}$$

Keywords

beta-dynamical systembeta-expansioninhomogeneous Diophantine approximationLebesgue measureHausdorff dimension

MSC classification

Primary: 11K55: Metric theory of other algorithms and expansions; measure and Hausdorff dimension
Secondary: 28A80: Fractals
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 91 , Issue 1 , February 2015 , pp. 34 - 40
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Besicovitch, A. S., ‘Sets of fractional dimension (IV): on rational approximation to real numbers’, J. Lond. Math. Soc. 9 (1934), 126–131.Google Scholar
Dajani, K. and Kraaikamp, C., Ergodic Theory of Numbers, Carus Mathematical Monographs, 29 (The Mathematical Association of America, Washington, DC, 2002).CrossRefGoogle Scholar
Dodson, M. M., ‘A note on metric inhomogeneous Diophantine approximation’, J. Aust. Math. Soc. Ser. A 62 (1997), 175–185.CrossRefGoogle Scholar
Falconer, K., Fractal Geometry. Mathematical Foundations and Applications, 2nd edn (John Wiley, Chichester, 2003).Google Scholar
Gel’fond, A. O., ‘A common property of number systems’, Izv. Akad. Nauk 23 (1959), 809–814 (in Russian).Google Scholar
Hill, R. and Velani, S., ‘The ergodic theory of shrinking targets’, Invent. Math. 119 (1995), 175–198.Google Scholar
Jarník, V., ‘Diophantische approximationen und Hasudorffsches mass’, Mat. Sb. 36 (1929), 371–382.Google Scholar
Levesley, J., ‘A general inhomogeneous Jarník–Besicovitch theorem’, J. Number Theory 71 (1998), 65–80.Google Scholar
Li, B., Persson, T., Wang, B. W. and Wu, J., ‘Diophantine approximation of the orbit of 1 in the dynamical system of beta expansion’, Math. Z. 276 (2014), 799–827.Google Scholar
Parry, W., ‘On the 𝛽-expansion of real numbers’, Acta Math. Hungar. 11 (1960), 401–416.CrossRefGoogle Scholar
Persson, T. and Schmeling, J., ‘Dyadic Diophantine approximation and Katok’s horseshoe approximation’, Acta Arith. 132 (2008), 205–230.Google Scholar
Philipp, W., ‘Some metrical theorems in number theory’, Pacific J. Math. 20 (1967), 109–127.CrossRefGoogle Scholar
Rényi, A., ‘Representations for real numbers and their ergodic properties’, Acta Math. Hungar. 8 (1957), 477–493.CrossRefGoogle Scholar
Schmeling, J., ‘Symbolic dynamics for 𝛽-shifts and self-normal numbers’, Ergod. Th. & Dynam. Syst. 17 (1997), 675–694.Google Scholar
Schmidt, W., ‘A metrical theorem in Diophantine approximation’, Canad. J. Math. 12 (1960), 619–631.Google Scholar
Schmidt, W. M., ‘Metrical theorems on fractional parts of sequences’, Trans. Amer. Math. Soc. 110 (1964), 493–518.Google Scholar
Shen, L. M. and Wang, B. W., ‘Shrinking target problems for beta-dynamical system’, Sci. China Math. 56 (2013), 91–104.Google Scholar
Tan, B. and Wang, B. W., ‘Quantitive recurrence properties of beta dynamical systems’, Adv. Math. 228 (2011), 2071–2097.CrossRefGoogle Scholar