Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-26T23:17:44.155Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON GENERALISED WALL–SUN–SUN PRIMES

Part of: Elementary number theory Sequences and sets

Published online by Cambridge University Press:  28 February 2023

JOSHUA HARRINGTON Open the ORCID record for JOSHUA HARRINGTON [Opens in a new window]  and
LENNY JONES Open the ORCID record for LENNY JONES [Opens in a new window]
JOSHUA HARRINGTON
Affiliation:
Department of Mathematics, Cedar Crest College, Allentown, Pennsylvania, USA e-mail: [email protected]
LENNY JONES*
Affiliation:
Professor Emeritus of Mathematics, Department of Mathematics, Shippensburg University, Shippensburg, PA 17257, USA
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let a and b be positive integers and let 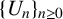$\{U_n\}_{n\ge 0}$ be the Lucas sequence of the first kind defined by

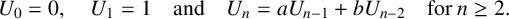$$ \begin{align*}U_0=0,\quad U_1=1\quad \mbox{and} \quad U_n=aU_{n-1}+bU_{n-2} \quad \mbox{for }n\ge 2.\end{align*} $$

We define an 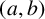$(a,b)$-Wall–Sun–Sun prime to be a prime p such that 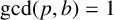$\gcd (p,b)=1$ and 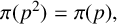$\pi (p^2)=\pi (p),$ where 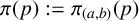$\pi (p):=\pi _{(a,b)}(p)$ is the length of the period of 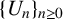$\{U_n\}_{n\ge 0}$ modulo p. When 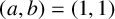$(a,b)=(1,1)$, such primes are known in the literature simply as Wall–Sun–Sun primes. In this note, we provide necessary and sufficient conditions such that a prime p dividing 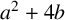$a^2+4b$ is an 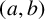$(a,b)$-Wall–Sun–Sun prime.

Keywords

Wall–Sun–Sun primeFibonacci–Wieferich primeLucas sequence

MSC classification

Primary: 11B39: Fibonacci and Lucas numbers and polynomials and generalizations
Secondary: 11A41: Primes
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 108 , Issue 3 , December 2023 , pp. 373 - 378
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bouazzaoui, Z., ‘Fibonacci numbers and real quadratic $p$ -rational fields’, Period. Math. Hungar. 81(1) (2020), 123–133.10.1007/s10998-020-00320-7CrossRefGoogle Scholar
Bouazzaoui, Z., ‘On periods of Fibonacci sequences and real quadratic p-rational fields’, Fibonacci Quart. 58(5) (2020), 103–110.Google Scholar
Crandall, R., Dilcher, K. and Pomerance, C., ‘A search for Wieferich and Wilson primes’, Math. Comp. 66(217) (1997), 433–449.10.1090/S0025-5718-97-00791-6CrossRefGoogle Scholar
Elsenhans, A.-S. and Jahnel, J., ‘The Fibonacci sequence modulo ${p}^2$ —An investigation by computer for $p<1014$ ’, Preprint, 2010, arXiv:1006.0824v1.Google Scholar
Jones, L., ‘A connection between the monogenicity of certain power-compositional trinomials and $k$ -Wall–Sun–Sun primes’, Preprint, 2022, arXiv:2211.14834.Google Scholar
Lucas sequence, https://en.wikipedia.org/wiki/Lucas sequence, Wikipedia, 2023.Google Scholar
Renault, M., ‘The period, rank, and order of the $\left(a,b\right)$ -Fibonacci sequence mod $m$ ’, Math. Mag. 86(5) (2013), 372–380.10.4169/math.mag.86.5.372CrossRefGoogle Scholar
Sun, Z. H. and Sun, Z. W., ‘Fibonacci numbers and Fermat’s last theorem’, Acta Arith. 60(4) (1992), 371–388.10.4064/aa-60-4-371-388CrossRefGoogle Scholar
Wall, D. D., ‘Fibonacci series modulo $m$ ’, Amer. Math. Monthly 67 (1960), 525–532.10.1080/00029890.1960.11989541CrossRefGoogle Scholar
Wall–Sun–Sun Prime, https://en.wikipedia.org/wiki/Wall--Sun--Sun prime, Wikipedia, 2022.Google Scholar
Wieferich Prime, https://en.wikipedia.org/wiki/Wieferich prime, Wikipedia, 2023.Google Scholar