Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-22T16:58:51.338Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on generalised linear complementarity problems

Published online by Cambridge University Press:  17 April 2009

J. Parida  and
B. Sahoo
J. Parida
Affiliation:
Department of Mathematics, Regional Engineering College, Rourkela, Orissa, India.
B. Sahoo
Affiliation:
Department of Mathematics, Regional Engineering College, Rourkela, Orissa, India.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given an n × n matrix A, an n-dimensional vector q, and a closed, convex cone S of Rn, the generalized linear complementarity problem considered here is the following: find a z ∈ Rn such that

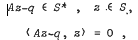
where s* is the polar cone of S. The existence of a solution to this problem for arbitrary vector q has been established both analytically and constructively for several classes of matrices A. In this note, a new class of matrices, denoted by J, is introduced. A is a J-matrix if

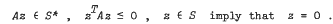
The new class can be seen to be broader than previously studied classes. We analytically show that for any A in this class, a solution to the above problem exists for arbitrary vector q. This is achieved by using a result on variational inequalities.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 18 , Issue 2 , April 1978 , pp. 161 - 168
Copyright
Copyright © Australian Mathematical Society 1978

References

[1]Bazaraa, M.S. and Goode, J.J., “Necessary optimality criteria in mathematical programming in the presence of differentiability”, J. Math. Anal. Appl. 40 (1972), 609–621.CrossRefGoogle Scholar
[2]Dantzig, G.B., Cottle, R.W., “Positive (semi-)definite programming”, Nonlinear programming, 55–73 (North-Holland, Amsterdam; Interscience [John Wiley & Sons], New York; 1967).Google Scholar
[3]Fiedler, Miroslav and Pták, Vlastimil, “On matrices with non-positive off-diagonal elements and positive principal minors”, Czeohoslavak Math. J. 12 (1962), 382–400.CrossRefGoogle Scholar
[4]Habetler, G.J. and Price, A.L., “Existence theory for generalized nonlinear complementarity problems”, J. Optimization Theory Appl. 7 (1971), 223–239.CrossRefGoogle Scholar
[5]Hartman, Philip and Stampacchia, Guido, “On some non-linear elliptic differential-functional equations”, Acta Math. 115 (1966), 271–310.CrossRefGoogle Scholar
[6]Karamardian, S., “Generalized complementarity problem”, J. Optimization Theory Appl. 8 (1971), 161–168.CrossRefGoogle Scholar
[7]Karamardian, S., “The complementarity problem”, Math. Programming 2 (1972), 107–129.CrossRefGoogle Scholar
[8]Parida, J. and Sahoo, B., “On the complex nonlinear complementarity problem”, Bull. Austral. Math. Soc. 14 (1976), 129–136.CrossRefGoogle Scholar
[9]Parida, J. and Sahoo, B., “Existence theory for the complex nonlinear complementarity problem”, Bull. Austral. Math. Soc. 14 (1976), 417–423.CrossRefGoogle Scholar