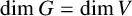1 Introduction
The problem of deciding which Lie groups are affinely flat (meaning they admit a left-invariant affine connection with zero curvature and torsion) has been studied for the past five decades, but a complete classification seems out of reach. In this paper we describe certain such groups that occur implicitly in the classification theory of nilpotent orbits. In doing so, we also take the opportunity to clarify the relations between different approaches to this classification theory. This connects to Ernest Vinberg’s work in two ways. The first is through Vinberg’s work on homogeneous cones [Reference Vinberg23] and his development of left-symmetric algebras, which are an algebraic way of characterising affinely flat Lie groups through an additional algebraic structure on their Lie algebras. The second is through Vinberg’s classification theory [Reference Vinberg24] of nilpotent orbits in semisimple Lie algebras, which uses a construction of certain Lie algebras of affinely flat reductive groups.
We focus on this second aspect in this paper. The original work on nilpotent orbit classifications by Vinberg [Reference Vinberg24] and by Bala and Carter [Reference Bala and Carter2, Reference Bala and Carter3] is quite involved, and one aim of this paper is to provide a more accessible and self-contained description of some of the main constructions in these papers. In addition to that, our discussion explains in detail the relation between these constructions. We also discuss an interesting connection to a construction of étale representations by Gyoja [Reference Gyoja15]. Our subject’s broad appeal comes from its relevance to research areas such as Lie theory, invariant theory and representation theory. Moreover, it has applications in mathematical physics. For example, certain flat affine connections on Lie groups correspond to the classical Yang–Baxter equation (see Bordemann [Reference Bordemann6]). Nilpotent orbit classifications, on the other hand, are useful tools in the study of supergravities and quantum information theory (see Dietrich et al. [Reference Dietrich, Faccin and de Graaf11, Reference Dietrich, de Graaf, Marrani and Origlia12]).
We start with a brief survey on reductive algebraic groups with étale representations (Section 1.1) and then describe the results and structure of this paper (Section 1.2).
1.1 Flat Lie groups and étale representations
The existence question for left-invariant flat affine connections on Lie groups first arose during the investigation of which Lie groups act (simply) transitively on an affine space (see Auslander [Reference Auslander1]) or, more generally, on subdomains of affine space, such as convex homogeneous cones (see Vinberg [Reference Vinberg23, Section I.6]). In these situations, the affinely flat Lie groups are always solvable. Indeed, geodesic completeness of the left-invariant flat affine connection is equivalent to the underlying simply connected Lie group acting simply transitively on an affine space, and this in turn is equivalent to the Lie group being solvable (see Milnor [Reference Milnor19, Theorem 3.2]). It was conjectured for some time that all nilpotent Lie groups are affinely flat, but this was eventually refuted by Benoist [Reference Benoist5].
A seminal paper by Medina Perea [Reference Medina Perea18] highlighted the equivalence of the existence of left-invariant flat affine connections on a Lie group, of left-symmetric products on its Lie algebra, and of affine étale representations of the Lie group or its Lie algebra. The latter are representations by affine transformations on an affine space of the same dimension as the group, such that there is an open orbit for the group action; these étale representations are a crucial tool in the analysis of affinely flat Lie groups. As they are best studied on Lie algebras, a Lie algebra is called affinely flat if it is the Lie algebra of an affinely flat group.
Eventually, there was interest in the (necessarily geodesically incomplete) affine structures on reductive algebraic groups. An example of an affinely flat structure on a reductive group is the general linear group
![]() $\mathrm {GL}(n)$
where the flat structure is induced through its multiplication action on the affine space of
$\mathrm {GL}(n)$
where the flat structure is induced through its multiplication action on the affine space of
![]() $n\times n$
matrices. The case of the reductive Lie algebra
$n\times n$
matrices. The case of the reductive Lie algebra
![]() $\mathfrak {gl}(n)$
was treated comprehensively by Baues [Reference Baues4] from the perspective of left-symmetric algebras, and Burde [Reference Burde7, Reference Burde8] showed that
$\mathfrak {gl}(n)$
was treated comprehensively by Baues [Reference Baues4] from the perspective of left-symmetric algebras, and Burde [Reference Burde7, Reference Burde8] showed that
![]() $\mathrm {GL}(n)$
is the only complex or split real affinely flat Lie group with one-dimensional centre and simple commutator subgroup.
$\mathrm {GL}(n)$
is the only complex or split real affinely flat Lie group with one-dimensional centre and simple commutator subgroup.
For a reductive group, every representation by affine transformations is in fact equivalent to a linear representation (see Milnor [Reference Milnor19, Lemma 2.3]), so we can and will henceforth take all étale representations for reductive groups or algebras to be linear representations. This frames the question for étale representations as a special case of the question for prehomogeneous modules for reductive algebraic groups. The latter is a module
![]() $(G,\varrho ,V)$
, where G is a reductive algebraic group G acting on a finite-dimensional complex vector space V through an algebraic representation
$(G,\varrho ,V)$
, where G is a reductive algebraic group G acting on a finite-dimensional complex vector space V through an algebraic representation
![]() $\varrho \colon G\to \mathrm {GL}(V)$
such that the G-action has a Zariski-open orbit on V; the points of this open orbit are said to be in general position in V. Then necessarily
$\varrho \colon G\to \mathrm {GL}(V)$
such that the G-action has a Zariski-open orbit on V; the points of this open orbit are said to be in general position in V. Then necessarily
![]() $\dim G\geqslant \dim V$
and we have an étale representation precisely if
$\dim G\geqslant \dim V$
and we have an étale representation precisely if
![]() $\dim G=\dim V$
. In this case we also call
$\dim G=\dim V$
. In this case we also call
![]() $(G,\varrho ,V)$
an étale module. Clearly, for étale modules, the stabiliser in G of any point in the open orbit is a finite subgroup. In terms of Lie algebras
$(G,\varrho ,V)$
an étale module. Clearly, for étale modules, the stabiliser in G of any point in the open orbit is a finite subgroup. In terms of Lie algebras
![]() $\mathfrak {g}$
, an étale representation is one where the action of
$\mathfrak {g}$
, an étale representation is one where the action of
![]() $\mathfrak {g}$
on a point in general position yields a vector space isomorphism between
$\mathfrak {g}$
on a point in general position yields a vector space isomorphism between
![]() $\mathfrak {g}$
and V; in particular,
$\mathfrak {g}$
and V; in particular,
![]() $\dim \mathfrak {g}=\dim V$
and the stabiliser subalgebra at a point in general position is trivial.
$\dim \mathfrak {g}=\dim V$
and the stabiliser subalgebra at a point in general position is trivial.
Since several classification results for prehomogeneous modules are available, this framework is well suited to the study of affinely flat reductive groups. The classification of irreducible prehomogeneous modules by Sato and Kimura [Reference Sato and Kimura21] allows us to find all irreducible étale representations for reductive groups simply by comparing dimensions in the Sato–Kimura classification. It is important to emphasise that nonirreducible étale modules cannot in general be written as a direct sum of irreducible étale modules. Some examples of nonirreducible prehomogeneous modules are given by Kimura et al. [Reference Kimura16, Reference Kimura, Kasai, Inuzuka and Yasukura17]. These partial classifications were summarised by Burde and Globke [Reference Burde and Globke9], who also discuss some obstructions to the existence of flat affine structures on reductive groups. Unfortunately, these examples do not point to a sensible structure theory for étale modules of reductive algebraic groups. On the other hand, it is remarkable that almost all simple factors appearing for the groups in these modules are of Lie type
![]() ${\mathrm {A}}$
, with the only exception being an occasional factor of type
${\mathrm {A}}$
, with the only exception being an occasional factor of type
![]() ${\mathrm {C}}_2$
.
${\mathrm {C}}_2$
.
With a comprehensive structure theory seeming far away, it is natural to ask which simple factors can appear in affinely flat reductive algebraic groups. This was further pursued in Burde et al. [Reference Burde, Globke and Minchenko10], where étale representations for certain reductive groups with one factor of either type
![]() ${\mathrm {B}}_n$
,
${\mathrm {B}}_n$
,
![]() ${\mathrm {C}}_n$
or
${\mathrm {C}}_n$
or
![]() ${\mathrm {D}}_n$
for arbitrary n were constructed. The examples with a factor of type
${\mathrm {D}}_n$
for arbitrary n were constructed. The examples with a factor of type
![]() ${\mathrm {C}}_n$
were particularly interesting, as their étale representations have not only finite, but trivial stabiliser. In particular, they provide a counterexample to a conjecture of Popov on the Zariski cancellation problem [Reference Popov, Kuoda, Onoda and Freudenburg20]. Moreover, in [Reference Burde, Globke and Minchenko10] it was shown that no reductive group with simple factors of type
${\mathrm {C}}_n$
were particularly interesting, as their étale representations have not only finite, but trivial stabiliser. In particular, they provide a counterexample to a conjecture of Popov on the Zariski cancellation problem [Reference Popov, Kuoda, Onoda and Freudenburg20]. Moreover, in [Reference Burde, Globke and Minchenko10] it was shown that no reductive group with simple factors of type
![]() ${\mathrm {F}}_4$
or
${\mathrm {F}}_4$
or
![]() ${\mathrm {E}}_8$
admits an étale representation.
${\mathrm {E}}_8$
admits an étale representation.
1.2 Overview of this paper
We focus on the étale representations for reductive algebraic groups arising in the classification of nilpotent orbits in semisimple Lie algebras, in particular, the classifications of Vinberg [Reference Vinberg24] and Bala and Carter [Reference Bala and Carter2, Reference Bala and Carter3]. We show in Proposition 2.1 that these groups are subject to certain restrictions, notably that all their simple factors are either special linear or orthogonal groups. In light of known examples of groups with symplectic groups as simple factors, this shows that étale modules of this type are a proper subclass of the étale modules for general reductive algebraic groups. The classification methods of Vinberg and of Bala and Carter share some common ideas, and the second aim of this paper is to provide concise descriptions of these methods and to explain how they are related. In Section 2 we first look at Vinberg’s construction of carrier algebras for nilpotent elements in a graded Lie algebra. From the classification of simple carrier algebras we determine the types of reductive groups for which étale modules arise by this method. In Section 3, we show how Bala and Carter find minimal Levi subalgebras for a given nilpotent element in a semisimple Lie algebra and explain how it relates to Vinberg’s carrier algebras (see Proposition 3.2 and its corollary). In fact, we see that the two approaches coincide for
![]() $\mathbb{Z}$
-graded algebras. Lastly, we discuss Gyoja’s method [Reference Gyoja15], which describes how a prehomogeneous module
$\mathbb{Z}$
-graded algebras. Lastly, we discuss Gyoja’s method [Reference Gyoja15], which describes how a prehomogeneous module
![]() $(G,\varrho ,V)$
for a reductive algebraic group can be used to construct an étale module
$(G,\varrho ,V)$
for a reductive algebraic group can be used to construct an étale module
![]() $(G',\varrho ',V')$
for a reductive subgroup
$(G',\varrho ',V')$
for a reductive subgroup
![]() $G'\leq G$
and a quotient module
$G'\leq G$
and a quotient module
![]() $V'$
of V. We show in Proposition 4.1 how this method generalises the constructions of Vinberg and Bala and Carter.
$V'$
of V. We show in Proposition 4.1 how this method generalises the constructions of Vinberg and Bala and Carter.
1.3 Notation
All Lie algebras
![]() $\mathfrak {g}$
we consider are defined over the field of complex numbers. The centraliser of a subset
$\mathfrak {g}$
we consider are defined over the field of complex numbers. The centraliser of a subset
![]() $X\subseteq \mathfrak {g}$
in
$X\subseteq \mathfrak {g}$
in
![]() $\mathfrak {g}$
is
$\mathfrak {g}$
is
![]() $\mathfrak {z}_{\mathfrak {g}}(X)=\{y\in \mathfrak {g}: [y,X]=\{0\}\}$
and the normaliser is
$\mathfrak {z}_{\mathfrak {g}}(X)=\{y\in \mathfrak {g}: [y,X]=\{0\}\}$
and the normaliser is
![]() $\mathfrak {n}_{\mathfrak {g}}(X)=\{y\in \mathfrak {g} : [y,X]\subseteq \operatorname {{\mathrm {span}}}_{\mathbb {C}}(X)\}$
. An element
$\mathfrak {n}_{\mathfrak {g}}(X)=\{y\in \mathfrak {g} : [y,X]\subseteq \operatorname {{\mathrm {span}}}_{\mathbb {C}}(X)\}$
. An element
![]() $x\in \mathfrak {g}$
is nilpotent (or semisimple) if its adjoint representation
$x\in \mathfrak {g}$
is nilpotent (or semisimple) if its adjoint representation
![]() $\mathrm {ad}(x)$
on
$\mathrm {ad}(x)$
on
![]() $\mathfrak {g}$
is nilpotent (or semisimple). An algebraic group G is reductive if its maximal unipotent normal subgroup is trivial. Here we call a Lie algebra
$\mathfrak {g}$
is nilpotent (or semisimple). An algebraic group G is reductive if its maximal unipotent normal subgroup is trivial. Here we call a Lie algebra
![]() $\mathfrak {g}$
reductive if it is the Lie algebra of a reductive algebraic group, but other definitions exist (see [Reference Tauvel and Yu22, Section 20.5]). In this case
$\mathfrak {g}$
reductive if it is the Lie algebra of a reductive algebraic group, but other definitions exist (see [Reference Tauvel and Yu22, Section 20.5]). In this case
![]() $\mathfrak {g}=\mathfrak {z}\oplus \mathfrak {s}$
, where
$\mathfrak {g}=\mathfrak {z}\oplus \mathfrak {s}$
, where
![]() $\mathfrak {s}$
is the semisimple commutator subalgebra of
$\mathfrak {s}$
is the semisimple commutator subalgebra of
![]() $\mathfrak {g}$
and
$\mathfrak {g}$
and
![]() $\mathfrak {z}=\mathfrak {z}(\mathfrak {g})$
is the centre of
$\mathfrak {z}=\mathfrak {z}(\mathfrak {g})$
is the centre of
![]() $\mathfrak {g}$
. Let
$\mathfrak {g}$
. Let
![]() $n>0$
be an integer and
$n>0$
be an integer and
![]() $\mathbb{Z}_n=\{0,\ldots ,n-1\}$
, or
$\mathbb{Z}_n=\{0,\ldots ,n-1\}$
, or
![]() $n=\infty $
and
$n=\infty $
and
![]() $\mathbb{Z}_\infty =\mathbb{Z}$
. A Lie algebra
$\mathbb{Z}_\infty =\mathbb{Z}$
. A Lie algebra
![]() $\mathfrak {g}$
is
$\mathfrak {g}$
is
![]() $\mathbb{Z}_n$
-graded if
$\mathbb{Z}_n$
-graded if
![]() $\mathfrak {g}=\bigoplus \nolimits _{i\in \mathbb{Z}_n}\mathfrak {g}_i$
, where each
$\mathfrak {g}=\bigoplus \nolimits _{i\in \mathbb{Z}_n}\mathfrak {g}_i$
, where each
![]() $\mathfrak {g}_i\leq \mathfrak {g}$
is a subspace and
$\mathfrak {g}_i\leq \mathfrak {g}$
is a subspace and
![]() $[\mathfrak {g}_i,\mathfrak {g}_j]\subseteq \mathfrak {g}_{i+j}$
for all
$[\mathfrak {g}_i,\mathfrak {g}_j]\subseteq \mathfrak {g}_{i+j}$
for all
![]() $i,j$
; here
$i,j$
; here
![]() $\mathfrak {g}_k=\mathfrak {g}_{k\bmod n}$
for all
$\mathfrak {g}_k=\mathfrak {g}_{k\bmod n}$
for all
![]() $k\in \mathbb{Z}$
. Note that
$k\in \mathbb{Z}$
. Note that
![]() $\mathfrak {g}_0$
is a subalgebra of
$\mathfrak {g}_0$
is a subalgebra of
![]() $\mathfrak {g}$
.
$\mathfrak {g}$
.
2 Vinberg’s carrier algebras
Vinberg [Reference Vinberg24] studied complex semisimple Lie algebras graded by an arbitrary abelian group. However, the first step in his analysis is to restrict to a subalgebra graded by a cyclic group, so we will only consider this case. Let
![]() $\mathfrak {g}$
be a
$\mathfrak {g}$
be a
![]() $\mathbb{Z}_n$
-graded semisimple Lie algebra, where
$\mathbb{Z}_n$
-graded semisimple Lie algebra, where
![]() $n>0$
is an integer or
$n>0$
is an integer or
![]() $n=\infty $
. If n is finite, then such a grading is the eigenspace decomposition of a Lie algebra automorphism of order n. If
$n=\infty $
. If n is finite, then such a grading is the eigenspace decomposition of a Lie algebra automorphism of order n. If
![]() $n=\infty $
, then the
$n=\infty $
, then the
![]() $\mathbb {Z}$
-grading of
$\mathbb {Z}$
-grading of
![]() $\mathfrak {g}$
comes from a derivation
$\mathfrak {g}$
comes from a derivation
![]() $\varphi $
that acts as multiplication by i on each
$\varphi $
that acts as multiplication by i on each
![]() $\mathfrak {g}_i$
. For semisimple
$\mathfrak {g}_i$
. For semisimple
![]() $\mathfrak {g}$
, this derivation is inner, that is,
$\mathfrak {g}$
, this derivation is inner, that is,
![]() $\varphi =\mathrm {ad}(h)$
for a unique defining element
$\varphi =\mathrm {ad}(h)$
for a unique defining element
![]() $h\in \mathfrak {g}_0$
.
$h\in \mathfrak {g}_0$
.
2.1 Carrier algebras
Carrier algebras for
![]() $\mathfrak {g}$
are constructed as follows. For a nonzero nilpotent
$\mathfrak {g}$
are constructed as follows. For a nonzero nilpotent
![]() $e\in \mathfrak {g}_1$
choose an
$e\in \mathfrak {g}_1$
choose an
![]() $\mathfrak {sl}_2$
-triple
$\mathfrak {sl}_2$
-triple
![]() $(h,e,f)$
where
$(h,e,f)$
where
![]() $h\in \mathfrak {g}_0$
and
$h\in \mathfrak {g}_0$
and
![]() $f\in \mathfrak {g}_{-1}$
; this means
$f\in \mathfrak {g}_{-1}$
; this means
![]() $[h,e]=2e$
,
$[h,e]=2e$
,
![]() $[h,f]=-2f$
and
$[h,f]=-2f$
and
![]() $[e,f]=h$
. Let
$[e,f]=h$
. Let
![]() $\mathfrak {t}_0$
be a maximal toral subalgebra of the centraliser of
$\mathfrak {t}_0$
be a maximal toral subalgebra of the centraliser of
![]() $(h,e,f)$
in
$(h,e,f)$
in
![]() $\mathfrak {g}_0$
and define
$\mathfrak {g}_0$
and define
![]() $\mathfrak {t}=\mathbb {C} h\oplus \mathfrak {t}_0$
. Equivalently,
$\mathfrak {t}=\mathbb {C} h\oplus \mathfrak {t}_0$
. Equivalently,
![]() $\mathfrak {t}$
is a maximal toral subalgebra of the normaliser of
$\mathfrak {t}$
is a maximal toral subalgebra of the normaliser of
![]() $\mathbb {C} e$
in
$\mathbb {C} e$
in
![]() $\mathfrak {g}_0$
(see [Reference Dietrich, de Graaf, Ruggeri and Trigiante13, Lemma 30]), where
$\mathfrak {g}_0$
(see [Reference Dietrich, de Graaf, Ruggeri and Trigiante13, Lemma 30]), where
![]() $\mathbb {C} e$
denotes the
$\mathbb {C} e$
denotes the
![]() $\mathbb {C}$
-span of e. Now let
$\mathbb {C}$
-span of e. Now let
![]() $\lambda \colon \mathfrak {t}\to \mathbb {C}$
such that
$\lambda \colon \mathfrak {t}\to \mathbb {C}$
such that
![]() $[t,e]=\lambda (t)e$
for all
$[t,e]=\lambda (t)e$
for all
![]() $t\in \mathfrak {t}$
, and define the
$t\in \mathfrak {t}$
, and define the
![]() $\mathbb {Z}$
-graded algebra
$\mathbb {Z}$
-graded algebra
![]() $\mathfrak {g}(\mathfrak {t},e)$
by
$\mathfrak {g}(\mathfrak {t},e)$
by
The derived subalgebra of
![]() $\mathfrak {g}(\mathfrak {t},e)$
is the carrier algebra of e, denoted by
$\mathfrak {g}(\mathfrak {t},e)$
is the carrier algebra of e, denoted by
It is
![]() $\mathbb {Z}$
-graded with the induced grading; note that
$\mathbb {Z}$
-graded with the induced grading; note that
![]() $e\in \mathfrak {c}(e)_1$
. This carrier algebra of e is unique up to conjugacy under the adjoint group
$e\in \mathfrak {c}(e)_1$
. This carrier algebra of e is unique up to conjugacy under the adjoint group
![]() $G_0$
of
$G_0$
of
![]() $\mathfrak {g}_0$
; one therefore also speaks of the carrier algebra of e in
$\mathfrak {g}_0$
; one therefore also speaks of the carrier algebra of e in
![]() $\mathfrak {g}$
. Moreover, two nonzero nilpotent elements of
$\mathfrak {g}$
. Moreover, two nonzero nilpotent elements of
![]() $\mathfrak {g}_1$
are
$\mathfrak {g}_1$
are
![]() $G_0$
-conjugate if and only if their carrier algebras are
$G_0$
-conjugate if and only if their carrier algebras are
![]() $G_0$
-conjugate, which makes carrier algebras a useful tool for classifying nilpotent orbits (see Vinberg [Reference Vinberg24, Section 4]). For details on the classification of nilpotent orbits in real semisimple Lie algebras using carrier algebras defined over the real field we refer to Dietrich et al. [Reference Dietrich, de Graaf, Marrani and Origlia12, Reference Dietrich, de Graaf, Ruggeri and Trigiante13].
$G_0$
-conjugate, which makes carrier algebras a useful tool for classifying nilpotent orbits (see Vinberg [Reference Vinberg24, Section 4]). For details on the classification of nilpotent orbits in real semisimple Lie algebras using carrier algebras defined over the real field we refer to Dietrich et al. [Reference Dietrich, de Graaf, Marrani and Origlia12, Reference Dietrich, de Graaf, Ruggeri and Trigiante13].
Vinberg [Reference Vinberg24, Theorem 4] showed that every carrier algebra is semisimple
![]() $\mathbb {Z}$
-graded with
$\mathbb {Z}$
-graded with
![]() $\mathfrak {c}(e)_k\leq \mathfrak {g}_k$
for each
$\mathfrak {c}(e)_k\leq \mathfrak {g}_k$
for each
![]() $k\in \mathbb {Z}$
, and that carrier algebras are characterised by the following three conditions:
$k\in \mathbb {Z}$
, and that carrier algebras are characterised by the following three conditions:
-
(V1)
 $\dim \mathfrak {c}(e)_0=\dim \mathfrak {c}(e)_1$
;
$\dim \mathfrak {c}(e)_0=\dim \mathfrak {c}(e)_1$
; -
(V2)
 $\mathfrak {c}(e)$
is normalised by a maximal toral subalgebra of
$\mathfrak {c}(e)$
is normalised by a maximal toral subalgebra of
 $\mathfrak {g}_0$
;
$\mathfrak {g}_0$
; -
(V3)
 $\mathfrak {c}(e)$
is not a proper subalgebra of a reductive
$\mathfrak {c}(e)$
is not a proper subalgebra of a reductive
 $\mathbb{Z}$
-graded subalgebra of
$\mathbb{Z}$
-graded subalgebra of
 $\mathfrak {g}$
of the same rank.
$\mathfrak {g}$
of the same rank.
Moreover, [Reference Vinberg24, Theorem 2] shows that e is in generic (or general) position in
![]() $\mathfrak {c}(e)_1$
, that is,
$\mathfrak {c}(e)_1$
, that is,
![]() $[\mathfrak {c}(e)_0,e]=\mathfrak {c}(e)_1$
, so (V1) states that the adjoint action of
$[\mathfrak {c}(e)_0,e]=\mathfrak {c}(e)_1$
, so (V1) states that the adjoint action of
![]() $\mathfrak {c}(e)_0$
on
$\mathfrak {c}(e)_0$
on
![]() $\mathfrak {c}(e)_1$
yields an étale representation for
$\mathfrak {c}(e)_1$
yields an étale representation for
![]() $\mathfrak {c}(e)_0$
.
$\mathfrak {c}(e)_0$
.
Only property (V1) is intrinsic to
![]() $\mathfrak {c}(e)$
, whereas (V2) and (V3) are determined by its embedding in the ambient Lie algebra
$\mathfrak {c}(e)$
, whereas (V2) and (V3) are determined by its embedding in the ambient Lie algebra
![]() $\mathfrak {g}$
. Thus, to describe the Lie algebras that can appear as carrier algebras for nilpotent elements in semisimple Lie algebras, one must merely classify
$\mathfrak {g}$
. Thus, to describe the Lie algebras that can appear as carrier algebras for nilpotent elements in semisimple Lie algebras, one must merely classify
![]() $\mathbb{Z}$
-graded Lie algebras with (V1); we call such an algebra an abstract carrier algebra. Every abstract carrier algebra is a direct sum of simple abstract carrier algebras, so to describe the possible étale modules
$\mathbb{Z}$
-graded Lie algebras with (V1); we call such an algebra an abstract carrier algebra. Every abstract carrier algebra is a direct sum of simple abstract carrier algebras, so to describe the possible étale modules
![]() $(\mathfrak {c}(e)_0,\mathrm {ad},\mathfrak {c}(e)_1)$
coming from semisimple carrier algebras, it is sufficient to focus on simple abstract carrier algebras in Lie algebras. In the next section we follow Djokovič’s description [Reference Djokovič14] (based on work by Vinberg [Reference Vinberg24]) of the classification of all simple abstract carrier algebras. Using a different terminology, Bala and Carter [Reference Bala and Carter2] have also obtained a classification for the classical case. These classifications determine the following proposition.
$(\mathfrak {c}(e)_0,\mathrm {ad},\mathfrak {c}(e)_1)$
coming from semisimple carrier algebras, it is sufficient to focus on simple abstract carrier algebras in Lie algebras. In the next section we follow Djokovič’s description [Reference Djokovič14] (based on work by Vinberg [Reference Vinberg24]) of the classification of all simple abstract carrier algebras. Using a different terminology, Bala and Carter [Reference Bala and Carter2] have also obtained a classification for the classical case. These classifications determine the following proposition.
Proposition 2.1. A reductive Lie algebra
![]() $\mathfrak {g}_0$
admitting an étale representation coming from the adjoint action of a nilpotent element is a direct sum of the degree-
$\mathfrak {g}_0$
admitting an étale representation coming from the adjoint action of a nilpotent element is a direct sum of the degree-
![]() $0$
components of
$0$
components of
![]() $j\geqslant 1$
simple abstract carrier algebras. As such, the semisimple part of
$j\geqslant 1$
simple abstract carrier algebras. As such, the semisimple part of
![]() $\mathfrak {g}_0$
, if nontrivial, has simple factors of type
$\mathfrak {g}_0$
, if nontrivial, has simple factors of type
![]() ${\mathrm {A}}$
and at most j factors of type
${\mathrm {A}}$
and at most j factors of type
![]() ${\mathrm {B}}$
or
${\mathrm {B}}$
or
![]() ${\mathrm {D}}$
. The centre of
${\mathrm {D}}$
. The centre of
![]() $\mathfrak {g}_0$
has dimension higher than j, unless all the simple abstract carrier algebras involved have weighted Dynkin diagrams of types in
$\mathfrak {g}_0$
has dimension higher than j, unless all the simple abstract carrier algebras involved have weighted Dynkin diagrams of types in
![]() $\{{\mathrm {A}}_1,{\mathrm {E}}_8^{(11)},{\mathrm {F}}_4^{(4)},{\mathrm {G}}_2^{(2)}\}$
as defined in [
Reference Djokovič14, Table II], in which case the centre of
$\{{\mathrm {A}}_1,{\mathrm {E}}_8^{(11)},{\mathrm {F}}_4^{(4)},{\mathrm {G}}_2^{(2)}\}$
as defined in [
Reference Djokovič14, Table II], in which case the centre of
![]() $\mathfrak {g}_0$
has dimension j.
$\mathfrak {g}_0$
has dimension j.
From Burde et al. [Reference Burde, Globke and Minchenko10] we know that there exist étale representations for reductive algebraic groups with a simple factor of type
![]() ${\mathrm {C}}$
. This shows the following corollary.
${\mathrm {C}}$
. This shows the following corollary.
Corollary 2.2. There are étale representations for reductive Lie algebras that do not come from the adjoint action of a nilpotent element.
2.2 Simple abstract carrier algebras Lie algebras
Recall that the grading of a semisimple
![]() $\mathbb {Z}$
-graded Lie algebra
$\mathbb {Z}$
-graded Lie algebra
![]() $\mathfrak {g}$
with defining element
$\mathfrak {g}$
with defining element
![]() $h\in \mathfrak {g}$
is determined by
$h\in \mathfrak {g}$
is determined by
![]() $\mathfrak {g}_k=\{x\in \mathfrak {g} : [h,x]=kx\}$
for
$\mathfrak {g}_k=\{x\in \mathfrak {g} : [h,x]=kx\}$
for
![]() $k\in \mathbb {Z}$
. Two
$k\in \mathbb {Z}$
. Two
![]() $\mathbb {Z}$
-graded Lie algebras
$\mathbb {Z}$
-graded Lie algebras
![]() $\mathfrak {g}$
and
$\mathfrak {g}$
and
![]() $\mathfrak {g}'$
with defining elements h and
$\mathfrak {g}'$
with defining elements h and
![]() $h'$
are isomorphic if there is a Lie algebra isomorphism
$h'$
are isomorphic if there is a Lie algebra isomorphism
![]() $\varphi \colon \mathfrak {g}\to \mathfrak {g}'$
with
$\varphi \colon \mathfrak {g}\to \mathfrak {g}'$
with
![]() $\varphi (h)=h'$
. Djokovič [Reference Djokovič14] classified, up to isomorphism, semisimple
$\varphi (h)=h'$
. Djokovič [Reference Djokovič14] classified, up to isomorphism, semisimple
![]() $\mathbb {Z}$
-graded Lie algebras in terms of weighted Dynkin diagrams. Let
$\mathbb {Z}$
-graded Lie algebras in terms of weighted Dynkin diagrams. Let
![]() $\mathfrak {h}\leq \mathfrak {g}$
be a maximal toral subalgebra containing h, with corresponding root system
$\mathfrak {h}\leq \mathfrak {g}$
be a maximal toral subalgebra containing h, with corresponding root system
![]() $\Phi $
. Let
$\Phi $
. Let
![]() $\Pi $
be a basis of simple roots such that
$\Pi $
be a basis of simple roots such that
![]() $\alpha (h)\geqslant 0$
for every
$\alpha (h)\geqslant 0$
for every
![]() $\alpha \in \Pi $
. Let
$\alpha \in \Pi $
. Let
![]() $\Delta (\mathfrak {g})$
be the Dynkin diagram of
$\Delta (\mathfrak {g})$
be the Dynkin diagram of
![]() $\mathfrak {g}$
with respect to
$\mathfrak {g}$
with respect to
![]() $\mathfrak {h}$
, with vertices labelled by
$\mathfrak {h}$
, with vertices labelled by
![]() $\Pi $
, and to each vertex
$\Pi $
, and to each vertex
![]() $\alpha \in \Pi $
attach the integer
$\alpha \in \Pi $
attach the integer
![]() $\alpha (h)$
. The resulting weighted Dynkin diagram is denoted by
$\alpha (h)$
. The resulting weighted Dynkin diagram is denoted by
![]() $\Delta (\mathfrak {g},h)$
. Now [Reference Djokovič14, Theorem 1] shows that there is a bijection between (isomorphism classes of)
$\Delta (\mathfrak {g},h)$
. Now [Reference Djokovič14, Theorem 1] shows that there is a bijection between (isomorphism classes of)
![]() $\mathbb {Z}$
-graded semisimple Lie algebras
$\mathbb {Z}$
-graded semisimple Lie algebras
![]() $(\mathfrak {g},h)$
and (isomorphism classes of) weighted Dynkin diagrams
$(\mathfrak {g},h)$
and (isomorphism classes of) weighted Dynkin diagrams
![]() $\Delta (\mathfrak {g},h)$
.
$\Delta (\mathfrak {g},h)$
.
In the following, let
![]() $(\mathfrak {g},h)$
be simple
$(\mathfrak {g},h)$
be simple
![]() $\mathbb{Z}$
-graded and define
$\mathbb{Z}$
-graded and define
![]() $\deg \alpha \in \mathbb{Z}$
for
$\deg \alpha \in \mathbb{Z}$
for
![]() $\alpha \in \Phi $
by
$\alpha \in \Phi $
by
![]() $x_\alpha \in \mathfrak {g}_{\deg \alpha }$
, where
$x_\alpha \in \mathfrak {g}_{\deg \alpha }$
, where
![]() $x_\alpha \in \mathfrak {g}$
is a root vector corresponding to
$x_\alpha \in \mathfrak {g}$
is a root vector corresponding to
![]() $\alpha $
. If
$\alpha $
. If
![]() $\deg \alpha =k$
, then
$\deg \alpha =k$
, then
![]() $\alpha (h)x_\alpha =[h,x_\alpha ]=kx_\alpha $
, hence
$\alpha (h)x_\alpha =[h,x_\alpha ]=kx_\alpha $
, hence
![]() $\alpha (h)=k$
; this shows that
$\alpha (h)=k$
; this shows that
![]() $\deg \alpha =\alpha (h)$
. If
$\deg \alpha =\alpha (h)$
. If
![]() $r_k$
is the number of roots with degree k, then
$r_k$
is the number of roots with degree k, then
![]() $\mathfrak {g}$
is an abstract carrier algebra if and only if
$\mathfrak {g}$
is an abstract carrier algebra if and only if
![]() $\dim \mathfrak {h} + r_0= r_1$
. It is shown in [Reference Djokovič14, page 374] that if
$\dim \mathfrak {h} + r_0= r_1$
. It is shown in [Reference Djokovič14, page 374] that if
![]() $\mathfrak {g}$
is an abstract carrier algebra, then
$\mathfrak {g}$
is an abstract carrier algebra, then
![]() $\deg \alpha \in \{0,1\}$
for every simple root
$\deg \alpha \in \{0,1\}$
for every simple root
![]() $\alpha \in \Pi $
. So for the classification it remains to determine the weighted Dynkin diagrams with weights
$\alpha \in \Pi $
. So for the classification it remains to determine the weighted Dynkin diagrams with weights
![]() $\{0,1\}$
such that
$\{0,1\}$
such that
![]() $\dim \mathfrak {h}_0+r_0=r_1$
. The reductive subalgebra
$\dim \mathfrak {h}_0+r_0=r_1$
. The reductive subalgebra
![]() $\mathfrak {g}_0$
is then given by the subdiagram consisting of the vertices with weight
$\mathfrak {g}_0$
is then given by the subdiagram consisting of the vertices with weight
![]() $0$
. To illustrate the method, we include the full proof for type A. To keep the exposition short, for the other types we only describe the results and refer to [Reference Djokovič14, Section 4], [Reference Bala and Carter2, Section 3] and [Reference Vinberg24, page 30] for more details.
$0$
. To illustrate the method, we include the full proof for type A. To keep the exposition short, for the other types we only describe the results and refer to [Reference Djokovič14, Section 4], [Reference Bala and Carter2, Section 3] and [Reference Vinberg24, page 30] for more details.
If
![]() $\mathfrak {g}_0=\mathfrak {h}$
is a maximal toral subalgebra, then
$\mathfrak {g}_0=\mathfrak {h}$
is a maximal toral subalgebra, then
![]() $r_0=0$
and all labels in the weighted diagram are
$r_0=0$
and all labels in the weighted diagram are
![]() $1$
; one says that
$1$
; one says that
![]() $\mathfrak {g}$
is principal. In this case the
$\mathfrak {g}$
is principal. In this case the
![]() $0$
-component of the carrier algebra is abelian.
$0$
-component of the carrier algebra is abelian.
Type A. Let
![]() $\mathfrak {g}=\mathfrak {sl}(n+1,\mathbb {C})$
. The diagonal matrix
$\mathfrak {g}=\mathfrak {sl}(n+1,\mathbb {C})$
. The diagonal matrix
![]() $h={\mathrm {diag}}(\lambda _1,\ldots ,\lambda _{n+1})$
is the defining element with
$h={\mathrm {diag}}(\lambda _1,\ldots ,\lambda _{n+1})$
is the defining element with
![]() $\lambda _1\geqslant \cdots \geqslant \lambda _{n+1}$
. Consider the root system
$\lambda _1\geqslant \cdots \geqslant \lambda _{n+1}$
. Consider the root system
![]() $\Phi =\{\pm (\varepsilon _i-\varepsilon _j) : 1\leq i<j<n\}$
and basis
$\Phi =\{\pm (\varepsilon _i-\varepsilon _j) : 1\leq i<j<n\}$
and basis
![]() $\Pi =\{\alpha _1,\ldots ,\alpha _n\}$
where each
$\Pi =\{\alpha _1,\ldots ,\alpha _n\}$
where each
![]() $\varepsilon _i$
maps h to
$\varepsilon _i$
maps h to
![]() $\lambda _i$
and
$\lambda _i$
and
![]() $\alpha _i=\varepsilon _i-\varepsilon _{i+1}$
. Let
$\alpha _i=\varepsilon _i-\varepsilon _{i+1}$
. Let
![]() $k= \lambda _1-\lambda _{n+1}$
and, for
$k= \lambda _1-\lambda _{n+1}$
and, for
![]() $i=0,\ldots ,k$
, let
$i=0,\ldots ,k$
, let
![]() $d_i$
be the number of
$d_i$
be the number of
![]() $\lambda _r$
with
$\lambda _r$
with
![]() $\lambda _r=\lambda _1-i$
. A root
$\lambda _r=\lambda _1-i$
. A root
![]() $\pm (\varepsilon _i-\varepsilon _j)$
has degree
$\pm (\varepsilon _i-\varepsilon _j)$
has degree
![]() $0$
if and only if
$0$
if and only if
![]() $\lambda _i=\lambda _j=\lambda _1-r$
for some r, and for each r there are
$\lambda _i=\lambda _j=\lambda _1-r$
for some r, and for each r there are
![]() $d_r(d_r-1)$
possibilities for
$d_r(d_r-1)$
possibilities for
![]() $\varepsilon _i$
and
$\varepsilon _i$
and
![]() $\varepsilon _j$
. This implies that
$\varepsilon _j$
. This implies that
![]() $r_0=\sum _{j=0}^k d_j(d_j-1)$
. In a similar way
$r_0=\sum _{j=0}^k d_j(d_j-1)$
. In a similar way
![]() $r_1=\sum _{j=0}^{k-1} d_jd_{j+1}$
, and now a direct calculation shows that
$r_1=\sum _{j=0}^{k-1} d_jd_{j+1}$
, and now a direct calculation shows that
![]() $n+r_0=r_1$
if and only if
$n+r_0=r_1$
if and only if
to see the latter, note that
![]() $d_0+\cdots +d_k=n+1$
. In conclusion,
$d_0+\cdots +d_k=n+1$
. In conclusion,
![]() $\mathfrak {g}$
is an abstract carrier algebra if and only if
$\mathfrak {g}$
is an abstract carrier algebra if and only if
![]() $d_0=\cdots =d_k=1$
and
$d_0=\cdots =d_k=1$
and
![]() $k=n$
, which is equivalent to
$k=n$
, which is equivalent to
![]() $\mathfrak {g}$
being principal.
$\mathfrak {g}$
being principal.
Types B and D. Let
![]() $\mathfrak {g}=\mathfrak {so}(m,\mathbb {C})$
be realised as
$\mathfrak {g}=\mathfrak {so}(m,\mathbb {C})$
be realised as
![]() $\mathfrak {g}=\{X\in \mathfrak {gl}(m,\mathbb {C}):X^\top J=-JX\}$
where J is the matrix with
$\mathfrak {g}=\{X\in \mathfrak {gl}(m,\mathbb {C}):X^\top J=-JX\}$
where J is the matrix with
![]() $1$
s on its anti-diagonal and
$1$
s on its anti-diagonal and
![]() $0$
s elsewhere, and either
$0$
s elsewhere, and either
![]() $m=2n+1$
(with
$m=2n+1$
(with
![]() $n\geqslant 2$
) or
$n\geqslant 2$
) or
![]() $m=2n$
(with
$m=2n$
(with
![]() $n\geqslant 4$
). Write the defining element as
$n\geqslant 4$
). Write the defining element as
![]() $h={\mathrm {diag}}(\lambda _1,\ldots ,\lambda _m)$
with
$h={\mathrm {diag}}(\lambda _1,\ldots ,\lambda _m)$
with
![]() $\lambda _1\geqslant \cdots \geqslant \lambda _m$
. Since
$\lambda _1\geqslant \cdots \geqslant \lambda _m$
. Since
![]() $hJ=-Jh$
, each
$hJ=-Jh$
, each
![]() $-\lambda _i = \lambda _{m+1-i}$
. It has been shown that there are
$-\lambda _i = \lambda _{m+1-i}$
. It has been shown that there are
![]() $s\geqslant 1$
and integers
$s\geqslant 1$
and integers
![]() $k_1>\cdots >k_s\geqslant 0$
such that, as multisets,
$k_1>\cdots >k_s\geqslant 0$
such that, as multisets,
and
![]() $m=(2k_1+1)+\cdots +(2k_s+1)$
; note that
$m=(2k_1+1)+\cdots +(2k_s+1)$
; note that
![]() $0$
occurs s times in
$0$
occurs s times in
![]() $\{\lambda _1,\ldots ,\lambda _m\}$
and
$\{\lambda _1,\ldots ,\lambda _m\}$
and
![]() $1$
occurs at least
$1$
occurs at least
![]() $s-1$
times, and so on. Conversely, for any such integers
$s-1$
times, and so on. Conversely, for any such integers
![]() $k_1>\cdots >k_s\geqslant 0$
with
$k_1>\cdots >k_s\geqslant 0$
with
![]() $m=(2k_1+1)+\cdots +(2k_s+1)$
there is a defining element h whose eigenvalues satisfy (2.2). To determine the labelled Dynkin diagrams, one chooses the diagonal matrices in
$m=(2k_1+1)+\cdots +(2k_s+1)$
there is a defining element h whose eigenvalues satisfy (2.2). To determine the labelled Dynkin diagrams, one chooses the diagonal matrices in
![]() $\mathfrak {g}$
as maximal toral subalgebra, and then the following statements hold.
$\mathfrak {g}$
as maximal toral subalgebra, and then the following statements hold.
If
![]() $m=2n+1$
, then s is odd and
$m=2n+1$
, then s is odd and
![]() $\lambda _{n+1}=0$
. The corresponding simple abstract carrier algebra
$\lambda _{n+1}=0$
. The corresponding simple abstract carrier algebra
![]() $B(k_1,\ldots ,k_s)$
of type
$B(k_1,\ldots ,k_s)$
of type
![]() ${\mathrm {B}}_n$
has a weighted Dynkin diagram with labels
${\mathrm {B}}_n$
has a weighted Dynkin diagram with labels
![]() $\lambda _1-\lambda _2,\ldots , \lambda _{n-1}-\lambda _n, \lambda _n$
, where
$\lambda _1-\lambda _2,\ldots , \lambda _{n-1}-\lambda _n, \lambda _n$
, where
![]() $\lambda _n$
is the label of the shorter root; see [Reference Djokovič14, Figure 5]. In that figure the last label is given as
$\lambda _n$
is the label of the shorter root; see [Reference Djokovič14, Figure 5]. In that figure the last label is given as
![]() $2\lambda _n$
which is a typo (see [Reference Bala and Carter2, pages 410–412]). If
$2\lambda _n$
which is a typo (see [Reference Bala and Carter2, pages 410–412]). If
![]() $s=1$
, then
$s=1$
, then
![]() $\{\lambda _1,\ldots ,\lambda _m\}=\{n,n-1,\ldots , 1-n,-n\}$
and
$\{\lambda _1,\ldots ,\lambda _m\}=\{n,n-1,\ldots , 1-n,-n\}$
and
![]() $B(n)$
is principal. If
$B(n)$
is principal. If
![]() $s=3$
, then
$s=3$
, then
![]() $\lambda _{n+1},\lambda _n=0$
and
$\lambda _{n+1},\lambda _n=0$
and
![]() $0<\lambda _{n-1}$
, implying that the semisimple part of
$0<\lambda _{n-1}$
, implying that the semisimple part of
![]() $\mathfrak {g}_0$
is a direct sum of algebras of type A. If
$\mathfrak {g}_0$
is a direct sum of algebras of type A. If
![]() $s\geqslant 5$
, then
$s\geqslant 5$
, then
![]() $\lambda _{n+1},\lambda _n,\lambda _{n-1}=0$
and that semisimple part is a direct sum of algebras of type A and one algebra of type B.
$\lambda _{n+1},\lambda _n,\lambda _{n-1}=0$
and that semisimple part is a direct sum of algebras of type A and one algebra of type B.
If
![]() $m=2n$
, then s is even and
$m=2n$
, then s is even and
![]() $\lambda _n=0$
. The corresponding abstract carrier algebra
$\lambda _n=0$
. The corresponding abstract carrier algebra
![]() $D(k_1,\ldots ,k_s)$
of type
$D(k_1,\ldots ,k_s)$
of type
![]() ${\mathrm {D}}_n$
has a weighted Dynkin diagram with labels
${\mathrm {D}}_n$
has a weighted Dynkin diagram with labels
![]() $\lambda _1-\lambda _2,\ldots , \lambda _{n-2}-\lambda _{n-1}, \lambda _{n-1},\lambda _{n-1}$
, where
$\lambda _1-\lambda _2,\ldots , \lambda _{n-2}-\lambda _{n-1}, \lambda _{n-1},\lambda _{n-1}$
, where
![]() $\lambda _{n-2}-\lambda _{n-1}$
is the label of the vertex of degree
$\lambda _{n-2}-\lambda _{n-1}$
is the label of the vertex of degree
![]() $3$
connected to the two vertices of degree 1 with label
$3$
connected to the two vertices of degree 1 with label
![]() $\lambda _{n-1}$
(see [Reference Djokovič14, Figure 6]). If
$\lambda _{n-1}$
(see [Reference Djokovič14, Figure 6]). If
![]() $s\geqslant 6$
, then
$s\geqslant 6$
, then
![]() $\lambda _n,\lambda _{n-1},\lambda _{n-2}=0$
and the semisimple part of
$\lambda _n,\lambda _{n-1},\lambda _{n-2}=0$
and the semisimple part of
![]() $\mathfrak {g}_0$
is a direct sum of algebras of type A and one algebra of type D. If
$\mathfrak {g}_0$
is a direct sum of algebras of type A and one algebra of type D. If
![]() $s=2$
and
$s=2$
and
![]() $k_2>0$
, or
$k_2>0$
, or
![]() $s=4$
, then that semisimple part is a direct sum of algebras of type A; if
$s=4$
, then that semisimple part is a direct sum of algebras of type A; if
![]() $s=2$
and
$s=2$
and
![]() $k_2=0$
, then
$k_2=0$
, then
![]() $D(n-1,0)$
is principal.
$D(n-1,0)$
is principal.
Type C. Let
![]() $\mathfrak {g}=\mathfrak {sp}(2n,\mathbb {C})$
be realised as
$\mathfrak {g}=\mathfrak {sp}(2n,\mathbb {C})$
be realised as
![]() $\mathfrak {g}=\{X\in \mathfrak {gl}(2n,\mathbb {C}):X^\top S=-SX\}$
where S has the identity matrix
$\mathfrak {g}=\{X\in \mathfrak {gl}(2n,\mathbb {C}):X^\top S=-SX\}$
where S has the identity matrix
![]() $I_n$
and the negative
$I_n$
and the negative
![]() $-I_n$
on its anti-diagonal. The simple abstract carrier algebras have the form
$-I_n$
on its anti-diagonal. The simple abstract carrier algebras have the form
![]() $C(k_1,\dots ,k_s)$
and the construction is similar to those for type B and D. Here we can assume the defining element is
$C(k_1,\dots ,k_s)$
and the construction is similar to those for type B and D. Here we can assume the defining element is
![]() $h={\mathrm {diag}}(\lambda _1,\ldots ,\lambda _n,-\lambda _n,\ldots ,-\lambda _1)$
with
$h={\mathrm {diag}}(\lambda _1,\ldots ,\lambda _n,-\lambda _n,\ldots ,-\lambda _1)$
with
![]() $\lambda _1\geqslant \cdots \geqslant \lambda _n>0$
and, as multisets,
$\lambda _1\geqslant \cdots \geqslant \lambda _n>0$
and, as multisets,
![]() $\{\pm \lambda _1,\ldots ,\pm \lambda _n\}=\{k_i-\tfrac {1}{2},k_i-\tfrac {3}{2},\ldots ,\tfrac {3}{2}-k_i,\tfrac {1}{2}-k_i : 1\leq i\leq s\}$
for some
$\{\pm \lambda _1,\ldots ,\pm \lambda _n\}=\{k_i-\tfrac {1}{2},k_i-\tfrac {3}{2},\ldots ,\tfrac {3}{2}-k_i,\tfrac {1}{2}-k_i : 1\leq i\leq s\}$
for some
![]() $k_1>k_2>\cdots > k_s>0$
with
$k_1>k_2>\cdots > k_s>0$
with
![]() $n=k_1+\cdots +k_n$
. If one chooses the diagonal matrices in
$n=k_1+\cdots +k_n$
. If one chooses the diagonal matrices in
![]() $\mathfrak {g}$
as maximal toral subalgebra, then the Dynkin diagram of
$\mathfrak {g}$
as maximal toral subalgebra, then the Dynkin diagram of
![]() $C(k_1,\ldots ,k_s)$
has labels
$C(k_1,\ldots ,k_s)$
has labels
![]() $\lambda _1-\lambda _2,\ldots ,\lambda _{n-1}-\lambda _n,2\lambda _n$
, where
$\lambda _1-\lambda _2,\ldots ,\lambda _{n-1}-\lambda _n,2\lambda _n$
, where
![]() $2\lambda _n$
is attached to the longer root (see [Reference Djokovič14, Figure 7]). Since
$2\lambda _n$
is attached to the longer root (see [Reference Djokovič14, Figure 7]). Since
![]() $\lambda _n\ne 0$
, we have
$\lambda _n\ne 0$
, we have
![]() $2\lambda _n=1$
, and so the semisimple part of
$2\lambda _n=1$
, and so the semisimple part of
![]() $\mathfrak {g}_0$
is a direct sum of algebras of type A. If
$\mathfrak {g}_0$
is a direct sum of algebras of type A. If
![]() $s=1$
, then
$s=1$
, then
![]() $C(n)$
is principal.
$C(n)$
is principal.
Exceptional types. A direct calculation yields the abstract carrier algebras
![]() $\mathfrak {g}$
of exceptional types
$\mathfrak {g}$
of exceptional types
![]() ${\mathrm {G}}_2$
,
${\mathrm {G}}_2$
,
![]() ${\mathrm {F}}_4$
,
${\mathrm {F}}_4$
,
![]() ${\mathrm {E}}_6$
,
${\mathrm {E}}_6$
,
![]() ${\mathrm {E}}_7$
,
${\mathrm {E}}_7$
,
![]() ${\mathrm {E}}_8$
; the semisimple part of
${\mathrm {E}}_8$
; the semisimple part of
![]() $\mathfrak {g}_0$
is always a sum of Lie algebras of type A (see [Reference Vinberg24, Table 1]).
$\mathfrak {g}_0$
is always a sum of Lie algebras of type A (see [Reference Vinberg24, Table 1]).
The centre of
![]() ${\mathfrak {g}_0}$
. Let
${\mathfrak {g}_0}$
. Let
![]() $\mathfrak {g}_0$
be as before and write
$\mathfrak {g}_0$
be as before and write
![]() $\mathfrak {g}_0=\mathfrak {z}\oplus \mathfrak {s}$
where
$\mathfrak {g}_0=\mathfrak {z}\oplus \mathfrak {s}$
where
![]() $\mathfrak {z}$
is the centre and
$\mathfrak {z}$
is the centre and
![]() $\mathfrak {s}$
is semisimple. It follows from [Reference Vinberg24, page 19] that
$\mathfrak {s}$
is semisimple. It follows from [Reference Vinberg24, page 19] that
![]() $\dim \mathfrak {z}=\operatorname {{\mathrm {rk}}}\mathfrak {g}_0-\operatorname {{\mathrm {rk}}}\mathfrak {s}=\operatorname {{\mathrm {rk}}}\mathfrak {g}-\operatorname {{\mathrm {rk}}}\mathfrak {s}$
. Since
$\dim \mathfrak {z}=\operatorname {{\mathrm {rk}}}\mathfrak {g}_0-\operatorname {{\mathrm {rk}}}\mathfrak {s}=\operatorname {{\mathrm {rk}}}\mathfrak {g}-\operatorname {{\mathrm {rk}}}\mathfrak {s}$
. Since
![]() $\operatorname {{\mathrm {rk}}} \mathfrak {s}$
equals the number of labels
$\operatorname {{\mathrm {rk}}} \mathfrak {s}$
equals the number of labels
![]() $0$
in the weighted Dynkin diagram of
$0$
in the weighted Dynkin diagram of
![]() $\mathfrak {g}$
, the dimension of
$\mathfrak {g}$
, the dimension of
![]() $\mathfrak {z}$
equals the number of labels
$\mathfrak {z}$
equals the number of labels
![]() $1$
. For example, if
$1$
. For example, if
![]() $\mathfrak {g}=B(5,2,1)$
with rank
$\mathfrak {g}=B(5,2,1)$
with rank
![]() $9$
, then
$9$
, then
![]() $\lambda _1,\ldots ,\lambda _9= 5,4,3,2,2,1,1,1,0$
, yielding labels
$\lambda _1,\ldots ,\lambda _9= 5,4,3,2,2,1,1,1,0$
, yielding labels
![]() $1,1,1,0,1,0,0,1,0$
; thus,
$1,1,1,0,1,0,0,1,0$
; thus,
![]() $\dim \mathfrak {z}=5$
. From the above classification, it follows that
$\dim \mathfrak {z}=5$
. From the above classification, it follows that
![]() $\dim \mathfrak {z}=1$
if and only if
$\dim \mathfrak {z}=1$
if and only if
![]() $\mathfrak {g}$
has type
$\mathfrak {g}$
has type
![]() ${\mathrm {A}}_1$
or if
${\mathrm {A}}_1$
or if
![]() $\mathfrak {g}$
is the
$\mathfrak {g}$
is the
![]() $\mathbb {Z}$
-graded algebra
$\mathbb {Z}$
-graded algebra
![]() ${\mathrm {E}}_8^{(11)}$
,
${\mathrm {E}}_8^{(11)}$
,
![]() ${\mathrm {F}}_4^{(4)}$
or
${\mathrm {F}}_4^{(4)}$
or
![]() ${\mathrm {G}}_2^{(2)}$
as defined in [Reference Djokovič14, Table II].
${\mathrm {G}}_2^{(2)}$
as defined in [Reference Djokovič14, Table II].
3 Bala and Carter’s construction
Bala and Carter [Reference Bala and Carter2, Reference Bala and Carter3] classified the nilpotent orbits in a complex simple Lie algebra using a construction very similar to Vinberg’s, without the assumption that the Lie algebras are graded. Just like Vinberg’s construction, this yields an étale representation for a certain reductive subalgebra of
![]() $\mathfrak {g}$
. In this section we review some of these results and show how the approaches by Vinberg and by Bala and Carter are related.
$\mathfrak {g}$
. In this section we review some of these results and show how the approaches by Vinberg and by Bala and Carter are related.
3.1 Minimal Levi subalgebras
First, we recall a few definitions. Let
![]() $\mathfrak {g}=\mathfrak {z}\oplus \mathfrak {s}$
be a reductive Lie algebra with
$\mathfrak {g}=\mathfrak {z}\oplus \mathfrak {s}$
be a reductive Lie algebra with
![]() $\mathfrak {s}$
semisimple and
$\mathfrak {s}$
semisimple and
![]() $\mathfrak {z}=\mathfrak {z}(\mathfrak {g})$
the centre. A Borel subalgebra of
$\mathfrak {z}=\mathfrak {z}(\mathfrak {g})$
the centre. A Borel subalgebra of
![]() $\mathfrak {g}$
is a maximal solvable subalgebra of
$\mathfrak {g}$
is a maximal solvable subalgebra of
![]() $\mathfrak {g}$
, and a subalgebra of
$\mathfrak {g}$
, and a subalgebra of
![]() $\mathfrak {g}$
is a parabolic subalgebra if it contains a Borel subalgebra of
$\mathfrak {g}$
is a parabolic subalgebra if it contains a Borel subalgebra of
![]() $\mathfrak {g}$
. Every parabolic subalgebra
$\mathfrak {g}$
. Every parabolic subalgebra
![]() $\mathfrak {p}$
of
$\mathfrak {p}$
of
![]() $\mathfrak {g}$
is a semidirect product
$\mathfrak {g}$
is a semidirect product
![]() $\mathfrak {p} = \mathfrak {m}\ltimes \mathfrak {n}$
of a nilpotent ideal
$\mathfrak {p} = \mathfrak {m}\ltimes \mathfrak {n}$
of a nilpotent ideal
![]() $\mathfrak {n}$
of
$\mathfrak {n}$
of
![]() $\mathfrak {p}$
, all of whose elements are nilpotent, and a reductive subalgebra
$\mathfrak {p}$
, all of whose elements are nilpotent, and a reductive subalgebra
![]() $\mathfrak {m}$
. A parabolic subalgebra is distinguished if
$\mathfrak {m}$
. A parabolic subalgebra is distinguished if
![]() $\dim \mathfrak {n}/[\mathfrak {n},\mathfrak {n}]=\dim \mathfrak {m}$
. Any reductive subalgebra
$\dim \mathfrak {n}/[\mathfrak {n},\mathfrak {n}]=\dim \mathfrak {m}$
. Any reductive subalgebra
![]() $\mathfrak {m}$
of
$\mathfrak {m}$
of
![]() $\mathfrak {g}$
arising in this way for some parabolic subalgebra of
$\mathfrak {g}$
arising in this way for some parabolic subalgebra of
![]() $\mathfrak {g}$
is a Levi subalgebra in
$\mathfrak {g}$
is a Levi subalgebra in
![]() $\mathfrak {g}$
. Its commutator
$\mathfrak {g}$
. Its commutator
![]() $\mathfrak {c}=[\mathfrak {m},\mathfrak {m}]$
is semisimple of parabolic type. Bala and Carter defined the terms above for semisimple
$\mathfrak {c}=[\mathfrak {m},\mathfrak {m}]$
is semisimple of parabolic type. Bala and Carter defined the terms above for semisimple
![]() $\mathfrak {g}$
, but they carry over without change to reductive
$\mathfrak {g}$
, but they carry over without change to reductive
![]() $\mathfrak {g}$
.
$\mathfrak {g}$
.
For semisimple
![]() $\mathfrak {g}$
, it is shown in [Reference Bala and Carter3, Theorem 6.1] that the classification of nilpotent orbits is equivalent to the classification of conjugacy classes of pairs
$\mathfrak {g}$
, it is shown in [Reference Bala and Carter3, Theorem 6.1] that the classification of nilpotent orbits is equivalent to the classification of conjugacy classes of pairs
![]() $(\mathfrak {c},\mathfrak {q}_{\mathfrak {c}})$
, where
$(\mathfrak {c},\mathfrak {q}_{\mathfrak {c}})$
, where
![]() $\mathfrak {c}$
is semisimple subalgebra of parabolic type in
$\mathfrak {c}$
is semisimple subalgebra of parabolic type in
![]() $\mathfrak {g}$
and
$\mathfrak {g}$
and
![]() $\mathfrak {q}_{\mathfrak {c}}$
is a distinguished parabolic subalgebra of
$\mathfrak {q}_{\mathfrak {c}}$
is a distinguished parabolic subalgebra of
![]() $\mathfrak {c}$
. For a nonzero nilpotent element
$\mathfrak {c}$
. For a nonzero nilpotent element
![]() $e\in \mathfrak {g}$
with
$e\in \mathfrak {g}$
with
![]() $\mathfrak {sl}_2$
-triple
$\mathfrak {sl}_2$
-triple
![]() $(h,e,f)$
, define
$(h,e,f)$
, define
![]() $\mathfrak {g}_k=\{x\in \mathfrak {g} : [h,x]=kx\}$
for
$\mathfrak {g}_k=\{x\in \mathfrak {g} : [h,x]=kx\}$
for
![]() $k\in \mathbb {Z}$
; this furnishes
$k\in \mathbb {Z}$
; this furnishes
![]() $\mathfrak {g}$
with a
$\mathfrak {g}$
with a
![]() $\mathbb {Z}$
-grading. With this grading,
$\mathbb {Z}$
-grading. With this grading,
![]() $e\in \mathfrak {g}_2$
. The element e is distinguished in
$e\in \mathfrak {g}_2$
. The element e is distinguished in
![]() $\mathfrak {g}$
if
$\mathfrak {g}$
if
![]() $\mathrm {ad}(e)\colon \mathfrak {g}_0\to \mathfrak {g}_2$
is an isomorphism, that is, if e is in general position. If e is not distinguished in
$\mathrm {ad}(e)\colon \mathfrak {g}_0\to \mathfrak {g}_2$
is an isomorphism, that is, if e is in general position. If e is not distinguished in
![]() $\mathfrak {g}$
, then [Reference Bala and Carter3, Propositions 5.3 and 5.4] tell us how to construct a semisimple subalgebra
$\mathfrak {g}$
, then [Reference Bala and Carter3, Propositions 5.3 and 5.4] tell us how to construct a semisimple subalgebra
![]() $\mathfrak {c}$
of
$\mathfrak {c}$
of
![]() $\mathfrak {g}$
in which e is distinguished: if
$\mathfrak {g}$
in which e is distinguished: if
![]() $\mathfrak {h}_0$
is a maximal toral subalgebra of the centraliser of
$\mathfrak {h}_0$
is a maximal toral subalgebra of the centraliser of
![]() $(h,e,f)$
in
$(h,e,f)$
in
![]() $\mathfrak {g}$
, then
$\mathfrak {g}$
, then
are a minimal Levi subalgebra of
![]() $\mathfrak {g}$
containing e and a semisimple subalgebra of parabolic type, respectively, such that e is distinguished in
$\mathfrak {g}$
containing e and a semisimple subalgebra of parabolic type, respectively, such that e is distinguished in
![]() $\mathfrak {c}$
. The pair corresponding to e can be chosen to be
$\mathfrak {c}$
. The pair corresponding to e can be chosen to be
![]() $(\mathfrak {c},\mathfrak {q}_{\mathfrak {c}})$
, where
$(\mathfrak {c},\mathfrak {q}_{\mathfrak {c}})$
, where
![]() $\mathfrak {q}_{\mathfrak {c}}$
is the Jacobson–Morozov parabolic (see [Reference Bala and Carter2, Proposition 4.3] and [Reference Bala and Carter3, Theorem 6.1]). If G is a semisimple algebraic group with Lie algebra
$\mathfrak {q}_{\mathfrak {c}}$
is the Jacobson–Morozov parabolic (see [Reference Bala and Carter2, Proposition 4.3] and [Reference Bala and Carter3, Theorem 6.1]). If G is a semisimple algebraic group with Lie algebra
![]() $\mathfrak {g}$
, then
$\mathfrak {g}$
, then
![]() $\mathfrak {c}$
is determined uniquely up to the action by
$\mathfrak {c}$
is determined uniquely up to the action by
![]() $\mathrm {Z}_G(e)$
, the centraliser of e in
$\mathrm {Z}_G(e)$
, the centraliser of e in
![]() $\mathrm {Ad}_{\mathfrak {g}}(G)$
. Since e is distinguished in
$\mathrm {Ad}_{\mathfrak {g}}(G)$
. Since e is distinguished in
![]() $\mathfrak {c}$
, the
$\mathfrak {c}$
, the
![]() $\mathbb {Z}$
-grading of its
$\mathbb {Z}$
-grading of its
![]() $\mathfrak {sl}_2$
-triple in
$\mathfrak {sl}_2$
-triple in
![]() $\mathfrak {c}$
yields an étale representation for the adjoint action of the reductive subalgebra
$\mathfrak {c}$
yields an étale representation for the adjoint action of the reductive subalgebra
![]() $\mathfrak {c}_0$
on the subspace
$\mathfrak {c}_0$
on the subspace
![]() $\mathfrak {c}_2$
by evaluation at e. The adjoint action of
$\mathfrak {c}_2$
by evaluation at e. The adjoint action of
![]() $\mathfrak {g}$
integrates to that of G, and thus we obtain an étale representation of the reductive group with Lie algebra
$\mathfrak {g}$
integrates to that of G, and thus we obtain an étale representation of the reductive group with Lie algebra
![]() $\mathfrak {c}_0$
on the space
$\mathfrak {c}_0$
on the space
![]() $\mathfrak {c}_2$
.
$\mathfrak {c}_2$
.
The Borel and parabolic subalgebras of a reductive
![]() $\mathfrak {g}=\mathfrak {s}\oplus \mathfrak {z}$
as above are precisely
$\mathfrak {g}=\mathfrak {s}\oplus \mathfrak {z}$
as above are precisely
![]() $\mathfrak {z}\oplus \mathfrak {b}$
and
$\mathfrak {z}\oplus \mathfrak {b}$
and
![]() $\mathfrak {z}\oplus \mathfrak {p}$
, respectively, with
$\mathfrak {z}\oplus \mathfrak {p}$
, respectively, with
![]() $\mathfrak {b}\leq \mathfrak {s}$
a Borel subalgebra and
$\mathfrak {b}\leq \mathfrak {s}$
a Borel subalgebra and
![]() $\mathfrak {p}\leq \mathfrak {s}$
parabolic. It follows that the Levi subalgebras of
$\mathfrak {p}\leq \mathfrak {s}$
parabolic. It follows that the Levi subalgebras of
![]() $\mathfrak {g}$
are precisely
$\mathfrak {g}$
are precisely
![]() $\mathfrak {z}\oplus \mathfrak {m}$
, where
$\mathfrak {z}\oplus \mathfrak {m}$
, where
![]() $\mathfrak {m}$
is a Levi subalgebra of
$\mathfrak {m}$
is a Levi subalgebra of
![]() $\mathfrak {s}$
; moreover,
$\mathfrak {s}$
; moreover,
![]() $\mathfrak {m}$
is a minimal Levi subalgebra containing e in
$\mathfrak {m}$
is a minimal Levi subalgebra containing e in
![]() $\mathfrak {s}$
if and only if
$\mathfrak {s}$
if and only if
![]() $\mathfrak {z}\oplus \mathfrak {m}$
is a minimal Levi subalgebra containing e in
$\mathfrak {z}\oplus \mathfrak {m}$
is a minimal Levi subalgebra containing e in
![]() $\mathfrak {g}$
.
$\mathfrak {g}$
.
3.2 Relation to carrier algebras
We compare the Bala and Carter construction with Vinberg’s carrier algebras. Vinberg starts with a semisimple
![]() $\mathbb {Z}_n$
-graded Lie algebra
$\mathbb {Z}_n$
-graded Lie algebra
![]() $\mathfrak {g}=\bigoplus _{i\in \mathbb {Z}_n}\mathfrak {g}_i$
; recall that we allow
$\mathfrak {g}=\bigoplus _{i\in \mathbb {Z}_n}\mathfrak {g}_i$
; recall that we allow
![]() $\mathbb {Z}_\infty =\mathbb {Z}$
here. Let
$\mathbb {Z}_\infty =\mathbb {Z}$
here. Let
![]() $e\in \mathfrak {g}_1$
be nonzero nilpotent with
$e\in \mathfrak {g}_1$
be nonzero nilpotent with
![]() $\mathfrak {sl}_2$
-triple
$\mathfrak {sl}_2$
-triple
![]() $(h,e,f)$
such that
$(h,e,f)$
such that
![]() $h\in \mathfrak {g}_0$
and
$h\in \mathfrak {g}_0$
and
![]() $f\in \mathfrak {g}_{-1}$
and define
$f\in \mathfrak {g}_{-1}$
and define
![]() $\mathfrak {g}(\mathfrak {t},e)$
as in (2.1); as mentioned before,
$\mathfrak {g}(\mathfrak {t},e)$
as in (2.1); as mentioned before,
![]() $\mathfrak {t}$
is a maximal toral subalgebra of the normaliser
$\mathfrak {t}$
is a maximal toral subalgebra of the normaliser
![]() $\mathfrak {n}_{\mathfrak {g}_0}(e)$
and
$\mathfrak {n}_{\mathfrak {g}_0}(e)$
and
![]() $\lambda \colon \mathfrak {t}\to \mathbb {C}$
is defined by
$\lambda \colon \mathfrak {t}\to \mathbb {C}$
is defined by
![]() $[t,e]=\lambda (t)e$
. Let
$[t,e]=\lambda (t)e$
. Let
![]() $h_0=\tfrac 12h$
define the
$h_0=\tfrac 12h$
define the
![]() $\mathbb {Z}$
-graded algebra
$\mathbb {Z}$
-graded algebra
Note that
![]() $\mathfrak {t}\leq \mathfrak {g}(h_0)_0$
. It follows from [Reference Vinberg24, Lemmas 1 and 2] that
$\mathfrak {t}\leq \mathfrak {g}(h_0)_0$
. It follows from [Reference Vinberg24, Lemmas 1 and 2] that
![]() $\mathfrak {g}(h_0)$
and
$\mathfrak {g}(h_0)$
and
![]() $\mathfrak {g}(\mathfrak {t},e)$
are both reductive. Recall that
$\mathfrak {g}(\mathfrak {t},e)$
are both reductive. Recall that
![]() $\mathfrak {t}=\mathbb {C} h\oplus \mathfrak {t}_0$
, where
$\mathfrak {t}=\mathbb {C} h\oplus \mathfrak {t}_0$
, where
![]() $\mathfrak {t}_0$
is a maximal toral subalgebra of
$\mathfrak {t}_0$
is a maximal toral subalgebra of
![]() $\mathfrak {z}_{\mathfrak {g}_0}(h,e,f)$
. More precisely, we can state the following lemma.
$\mathfrak {z}_{\mathfrak {g}_0}(h,e,f)$
. More precisely, we can state the following lemma.
Lemma 3.1. We have
![]() $\mathfrak {t}_0=\ker \lambda =\mathfrak {z}(\mathfrak {g}(\mathfrak {t},e))$
and
$\mathfrak {t}_0=\ker \lambda =\mathfrak {z}(\mathfrak {g}(\mathfrak {t},e))$
and
![]() $\mathfrak {g}(\mathfrak {t},e)=\mathfrak {z}_{\mathfrak {g}(h_0)}(\mathfrak {t}_0)$
.
$\mathfrak {g}(\mathfrak {t},e)=\mathfrak {z}_{\mathfrak {g}(h_0)}(\mathfrak {t}_0)$
.
Proof. Write
![]() $\mathfrak {z}=\mathfrak {z}(\mathfrak {g}(\mathfrak {t},e))$
. Recall that
$\mathfrak {z}=\mathfrak {z}(\mathfrak {g}(\mathfrak {t},e))$
. Recall that
![]() $\mathfrak {t}=\mathbb {C} h\oplus \mathfrak {t}_0$
, so
$\mathfrak {t}=\mathbb {C} h\oplus \mathfrak {t}_0$
, so
![]() $\ker \lambda =\mathfrak {t}_0$
follows from
$\ker \lambda =\mathfrak {t}_0$
follows from
![]() $[h,e]=2e$
. Clearly, if
$[h,e]=2e$
. Clearly, if
![]() $t\in \ker \lambda $
, then
$t\in \ker \lambda $
, then
![]() $[t,y]=0$
for each
$[t,y]=0$
for each
![]() $y\in \mathfrak {g}(\mathfrak {t},e)_k$
, so
$y\in \mathfrak {g}(\mathfrak {t},e)_k$
, so
![]() $t\in \mathfrak {z}$
. Since
$t\in \mathfrak {z}$
. Since
![]() $\mathfrak {z}$
commutes with the defining element of
$\mathfrak {z}$
commutes with the defining element of
![]() $\mathfrak {g}(\mathfrak {t},e)$
, we have
$\mathfrak {g}(\mathfrak {t},e)$
, we have
![]() $\mathfrak {z}\leq \mathfrak {g}(\mathfrak {t},e)_0$
. Thus,
$\mathfrak {z}\leq \mathfrak {g}(\mathfrak {t},e)_0$
. Thus,
![]() $\mathfrak {z}\leq \mathfrak {n}_{\mathfrak {g}_0}(e)$
and therefore
$\mathfrak {z}\leq \mathfrak {n}_{\mathfrak {g}_0}(e)$
and therefore
![]() $\mathfrak {z}\leq \mathfrak {t}$
. This implies
$\mathfrak {z}\leq \mathfrak {t}$
. This implies
![]() $\mathfrak {z}\leq \ker \lambda $
, hence
$\mathfrak {z}\leq \ker \lambda $
, hence
![]() $\mathfrak {z}=\ker \lambda $
. Suppose
$\mathfrak {z}=\ker \lambda $
. Suppose
![]() $x\in \mathfrak {g}(h_0)$
centralises
$x\in \mathfrak {g}(h_0)$
centralises
![]() $\mathfrak {t}_0$
and write
$\mathfrak {t}_0$
and write
![]() $x=\bigoplus _{k\in \mathbb {Z}} x_k$
with each
$x=\bigoplus _{k\in \mathbb {Z}} x_k$
with each
![]() $x_k\in \mathfrak {g}(h_0)_k$
. Since
$x_k\in \mathfrak {g}(h_0)_k$
. Since
![]() $t_0\leq \mathfrak {g}(h_0)_0$
, it follows from
$t_0\leq \mathfrak {g}(h_0)_0$
, it follows from
![]() $0=[x,\mathfrak {t}_0]=\bigoplus _{k\in \mathbb {Z}} [x_k,\mathfrak {t}_0]$
that each
$0=[x,\mathfrak {t}_0]=\bigoplus _{k\in \mathbb {Z}} [x_k,\mathfrak {t}_0]$
that each
![]() $x_k$
centralises
$x_k$
centralises
![]() $\mathfrak {t}_0$
. By assumption,
$\mathfrak {t}_0$
. By assumption,
![]() $[h,x_k]=2kx_k$
, so
$[h,x_k]=2kx_k$
, so
![]() $x_k\in \mathfrak {g}(\mathfrak {t},e)_k$
and hence
$x_k\in \mathfrak {g}(\mathfrak {t},e)_k$
and hence
![]() $\mathfrak {z}_{\mathfrak {g}(h_0)}(\mathfrak {t}_0)\leq \mathfrak {g}(\mathfrak {t},e)$
. Conversely, if
$\mathfrak {z}_{\mathfrak {g}(h_0)}(\mathfrak {t}_0)\leq \mathfrak {g}(\mathfrak {t},e)$
. Conversely, if
![]() $x\in \mathfrak {g}(\mathfrak {t},e)_k$
then
$x\in \mathfrak {g}(\mathfrak {t},e)_k$
then
![]() $[h,x]=2kx$
, and if
$[h,x]=2kx$
, and if
![]() $t\in \mathfrak {t}_0$
then
$t\in \mathfrak {t}_0$
then
![]() $[t,x]=k\lambda (t)x=0$
since
$[t,x]=k\lambda (t)x=0$
since
![]() $\mathfrak {t}_0=\ker \lambda $
. Thus,
$\mathfrak {t}_0=\ker \lambda $
. Thus,
![]() $x\in \mathfrak {z}_{\mathfrak {g}(h_0)}(\mathfrak {t}_0)_k$
.
$x\in \mathfrak {z}_{\mathfrak {g}(h_0)}(\mathfrak {t}_0)_k$
.
The next proposition shows that Vinberg’s construction (2.1) of
![]() $\mathfrak {g}(\mathfrak {t},e)$
and its carrier algebra is the same as applying Bala and Carter’s approach (3.1) to the
$\mathfrak {g}(\mathfrak {t},e)$
and its carrier algebra is the same as applying Bala and Carter’s approach (3.1) to the
![]() $\mathbb{Z}$
-graded Lie algebra
$\mathbb{Z}$
-graded Lie algebra
![]() $\mathfrak {g}(h_0)$
. Below, let G be the semisimple algebraic group with Lie algebra
$\mathfrak {g}(h_0)$
. Below, let G be the semisimple algebraic group with Lie algebra
![]() $\mathfrak {g}(h_0)$
. The conjugacy up to the centraliser
$\mathfrak {g}(h_0)$
. The conjugacy up to the centraliser
![]() $\mathrm {Z}_G(e)$
reflects the freedom in choosing an
$\mathrm {Z}_G(e)$
reflects the freedom in choosing an
![]() $\mathfrak {sl}_2$
-triple
$\mathfrak {sl}_2$
-triple
![]() $(h,e,f)$
for a given nonzero nilpotent element e.
$(h,e,f)$
for a given nonzero nilpotent element e.
Proposition 3.2. Let
![]() $\mathfrak {g}$
be a
$\mathfrak {g}$
be a
![]() $\mathbb{Z}_n$
-graded complex semisimple Lie algebra, where
$\mathbb{Z}_n$
-graded complex semisimple Lie algebra, where
![]() $n\in \mathbb{N}\cup \{\infty \}$
, and let e,
$n\in \mathbb{N}\cup \{\infty \}$
, and let e,
![]() $h_0$
, and
$h_0$
, and
![]() $\mathfrak {t}$
be as above. Then
$\mathfrak {t}$
be as above. Then
![]() $\mathfrak {g}(\mathfrak {t},e)$
is a minimal Levi subalgebra of
$\mathfrak {g}(\mathfrak {t},e)$
is a minimal Levi subalgebra of
![]() $\mathfrak {g}(h_0)$
containing e and, up to
$\mathfrak {g}(h_0)$
containing e and, up to
![]() $\mathrm {Z}_G(e)$
-conjugacy, the carrier subalgebra
$\mathrm {Z}_G(e)$
-conjugacy, the carrier subalgebra
![]() $\mathfrak {c}(e)=[\mathfrak {g}(\mathfrak {t},e),\mathfrak {g}(\mathfrak {t},e)]$
is the unique semisimple subalgebra of parabolic type in
$\mathfrak {c}(e)=[\mathfrak {g}(\mathfrak {t},e),\mathfrak {g}(\mathfrak {t},e)]$
is the unique semisimple subalgebra of parabolic type in
![]() $\mathfrak {g}(h_0)$
in which e is distinguished.
$\mathfrak {g}(h_0)$
in which e is distinguished.
Proof. Note that h stabilises each
![]() $\mathfrak {g}_k$
and
$\mathfrak {g}_k$
and
![]() $\mathfrak {g}(h_0)_k$
is the intersection of
$\mathfrak {g}(h_0)_k$
is the intersection of
![]() $\mathfrak {g}_k$
with the
$\mathfrak {g}_k$
with the
![]() $2k$
-eigenspace of h. Lemma 3.1 shows that
$2k$
-eigenspace of h. Lemma 3.1 shows that
![]() $\mathfrak {g}(\mathfrak {t},e)\leq \mathfrak {g}(h_0)$
and the
$\mathfrak {g}(\mathfrak {t},e)\leq \mathfrak {g}(h_0)$
and the
![]() $\mathbb {Z}$
-gradings of both algebras are determined by the eigenvalues of
$\mathbb {Z}$
-gradings of both algebras are determined by the eigenvalues of
![]() $\mathrm {ad}(h_0)$
. The semisimple part
$\mathrm {ad}(h_0)$
. The semisimple part
![]() $\mathfrak {s}$
of
$\mathfrak {s}$
of
![]() $\mathfrak {g}(h_0)$
is a semisimple ideal in
$\mathfrak {g}(h_0)$
is a semisimple ideal in
![]() $\mathfrak {g}(h_0)$
containing
$\mathfrak {g}(h_0)$
containing
![]() $(h,e,f)$
; let
$(h,e,f)$
; let
![]() $\mathfrak {a}$
be the subalgebra generated by
$\mathfrak {a}$
be the subalgebra generated by
![]() $\{h,e,f\}$
. Note that for every subset
$\{h,e,f\}$
. Note that for every subset
![]() $X\subseteq \mathfrak {g}(h_0)$
,
$X\subseteq \mathfrak {g}(h_0)$
,
We claim that
![]() $\mathfrak {t}_0$
is a maximal toral subalgebra of
$\mathfrak {t}_0$
is a maximal toral subalgebra of
![]() $\mathfrak {z}_{\mathfrak {g}(h_0)}(\mathfrak {a})$
: recall that
$\mathfrak {z}_{\mathfrak {g}(h_0)}(\mathfrak {a})$
: recall that
![]() $\mathfrak {t}_0$
is defined as a maximal toral subalgebra of
$\mathfrak {t}_0$
is defined as a maximal toral subalgebra of
![]() $\mathfrak {z}_{\mathfrak {g}_0}(\mathfrak {a})$
, which is reductive by [Reference Vinberg24, page 21]. Since
$\mathfrak {z}_{\mathfrak {g}_0}(\mathfrak {a})$
, which is reductive by [Reference Vinberg24, page 21]. Since
![]() $\mathfrak {t}_0\leq \mathfrak {g}(h_0)_0\leq \mathfrak {g}_0$
, we know that
$\mathfrak {t}_0\leq \mathfrak {g}(h_0)_0\leq \mathfrak {g}_0$
, we know that
![]() $\mathfrak {t}_0$
is also a maximal toral subalgebra in
$\mathfrak {t}_0$
is also a maximal toral subalgebra in
![]() $\mathfrak {z}_{\mathfrak {g}(h_0)_0}(\mathfrak {a})$
. On the other hand,
$\mathfrak {z}_{\mathfrak {g}(h_0)_0}(\mathfrak {a})$
. On the other hand,
![]() $\mathfrak {z}_{\mathfrak {g}(h_0)_0}(\mathfrak {a})=\mathfrak {z}_{\mathfrak {g}(h_0)}(\mathfrak {a})$
because elements of nonzero degree in
$\mathfrak {z}_{\mathfrak {g}(h_0)_0}(\mathfrak {a})=\mathfrak {z}_{\mathfrak {g}(h_0)}(\mathfrak {a})$
because elements of nonzero degree in
![]() $\mathfrak {g}(h_0)$
do not commute with the defining element
$\mathfrak {g}(h_0)$
do not commute with the defining element
![]() $h_0\in \mathfrak {a}$
; thus,
$h_0\in \mathfrak {a}$
; thus,
![]() $\mathfrak {t}_0\leq \mathfrak {z}_{\mathfrak {g}(h_0)}(\mathfrak {a})$
is a maximal toral subalgebra. We can write
$\mathfrak {t}_0\leq \mathfrak {z}_{\mathfrak {g}(h_0)}(\mathfrak {a})$
is a maximal toral subalgebra. We can write
![]() $\mathfrak {t}_0 = \mathfrak {z}(\mathfrak {g}(h_0)) \oplus \mathfrak {t}_0'$
, where
$\mathfrak {t}_0 = \mathfrak {z}(\mathfrak {g}(h_0)) \oplus \mathfrak {t}_0'$
, where
![]() $\mathfrak {t}_0'$
is a maximal toral subalgebra of
$\mathfrak {t}_0'$
is a maximal toral subalgebra of
![]() $\mathfrak {z}_{\mathfrak {s}}(\mathfrak {a})$
, and so for every subset
$\mathfrak {z}_{\mathfrak {s}}(\mathfrak {a})$
, and so for every subset
![]() $X\subseteq \mathfrak {g}(h_0)$
,
$X\subseteq \mathfrak {g}(h_0)$
,
The construction in (3.1) shows that
![]() $\mathfrak {m}'=\mathfrak {z}_{\mathfrak {s}}(\mathfrak {t}_0')$
is a minimal Levi subalgebra of
$\mathfrak {m}'=\mathfrak {z}_{\mathfrak {s}}(\mathfrak {t}_0')$
is a minimal Levi subalgebra of
![]() $\mathfrak {s}$
containing e, so
$\mathfrak {s}$
containing e, so
![]() $\mathfrak {m}=\mathfrak {z}(\mathfrak {g}(h_0))\oplus \mathfrak {m}'$
is a minimal Levi subalgebra of
$\mathfrak {m}=\mathfrak {z}(\mathfrak {g}(h_0))\oplus \mathfrak {m}'$
is a minimal Levi subalgebra of
![]() $\mathfrak {g}(h_0)$
containing e. Now (*), (**) and Lemma 3.1 show
$\mathfrak {g}(h_0)$
containing e. Now (*), (**) and Lemma 3.1 show
so
![]() $\mathfrak {g}(\mathfrak {t},e)$
is a minimal Levi subalgebra in
$\mathfrak {g}(\mathfrak {t},e)$
is a minimal Levi subalgebra in
![]() $\mathfrak {g}(h_0)$
containing e. The construction in (3.1) shows that e is distinguished in
$\mathfrak {g}(h_0)$
containing e. The construction in (3.1) shows that e is distinguished in
![]() $[\mathfrak {m},\mathfrak {m}]$
and the latter is semisimple of parabolic type. Since
$[\mathfrak {m},\mathfrak {m}]$
and the latter is semisimple of parabolic type. Since
![]() $[\mathfrak {g}(\mathfrak {t},e),\mathfrak {g}(\mathfrak {t},e)]=[\mathfrak {m},\mathfrak {m}]$
is the carrier algebra, the claim follows; [Reference Bala and Carter3, Proposition 5.3] shows uniqueness up to
$[\mathfrak {g}(\mathfrak {t},e),\mathfrak {g}(\mathfrak {t},e)]=[\mathfrak {m},\mathfrak {m}]$
is the carrier algebra, the claim follows; [Reference Bala and Carter3, Proposition 5.3] shows uniqueness up to
![]() $\mathrm {Z}_G(e)$
-conjugacy.
$\mathrm {Z}_G(e)$
-conjugacy.
For a
![]() $\mathbb{Z}$
-graded semisimple Lie algebra
$\mathbb{Z}$
-graded semisimple Lie algebra
![]() $\mathfrak {g}$
, we have
$\mathfrak {g}$
, we have
![]() $\mathfrak {g}=\mathfrak {g}(h_0)$
where
$\mathfrak {g}=\mathfrak {g}(h_0)$
where
![]() $h=2h_0$
is the defining element (see [Reference Dietrich, de Graaf, Ruggeri and Trigiante13, Remark 33]), so the two approaches by Vinberg and Bala and Carter coincide.
$h=2h_0$
is the defining element (see [Reference Dietrich, de Graaf, Ruggeri and Trigiante13, Remark 33]), so the two approaches by Vinberg and Bala and Carter coincide.
Corollary 3.3. If
![]() $\mathfrak {g}$
is a
$\mathfrak {g}$
is a
![]() $\mathbb{Z}$
-graded complex semisimple Lie algebra, then up to
$\mathbb{Z}$
-graded complex semisimple Lie algebra, then up to
![]() $\mathrm {Z}_G(e)$
-conjugacy, the subalgebra
$\mathrm {Z}_G(e)$
-conjugacy, the subalgebra
![]() $\mathfrak {g}(\mathfrak {t},e)$
obtained by Vinberg’s construction and the subalgebra
$\mathfrak {g}(\mathfrak {t},e)$
obtained by Vinberg’s construction and the subalgebra
![]() $\mathfrak {m}$
obtained by Bala and Carter’s construction coincide.
$\mathfrak {m}$
obtained by Bala and Carter’s construction coincide.
Even in the situation where
![]() $\mathfrak {g}$
is given without a grading and e is a nonzero nilpotent element in
$\mathfrak {g}$
is given without a grading and e is a nonzero nilpotent element in
![]() $\mathfrak {g}$
, a choice of
$\mathfrak {g}$
, a choice of
![]() $h_0$
induces a
$h_0$
induces a
![]() $\mathbb{Z}$
-grading on
$\mathbb{Z}$
-grading on
![]() $\mathfrak {g}$
to which Vinberg’s approach can be applied; this is then equivalent to Bala and Carter’s approach. Note that Bala and Carter use the element h rather than
$\mathfrak {g}$
to which Vinberg’s approach can be applied; this is then equivalent to Bala and Carter’s approach. Note that Bala and Carter use the element h rather than
![]() $h_0=\tfrac 12h$
to define their grading, which leads to an additional factor of
$h_0=\tfrac 12h$
to define their grading, which leads to an additional factor of
![]() $2$
in the degrees.
$2$
in the degrees.
4 Gyoja’s construction
Gyoja [Reference Gyoja15] described constructions of étale modules out of a given prehomogeneous module. Let G be a complex reductive algebraic group with algebraic representation
![]() $\varrho \colon G\to \mathrm {GL}(V)$
on a finite-dimensional complex vector space V such that
$\varrho \colon G\to \mathrm {GL}(V)$
on a finite-dimensional complex vector space V such that
![]() $(G,\varrho ,V)$
is a prehomogeneous module. Let
$(G,\varrho ,V)$
is a prehomogeneous module. Let
![]() $v\in V$
be the point in general position. The construction in [Reference Gyoja15, Theorem A] proceeds as follows. Let
$v\in V$
be the point in general position. The construction in [Reference Gyoja15, Theorem A] proceeds as follows. Let
![]() $G_v$
be the stabiliser of v in G with Cartan subgroup
$G_v$
be the stabiliser of v in G with Cartan subgroup
![]() $T\leq G_v$
, define
$T\leq G_v$
, define
![]() $G'=\mathrm {N}_G(T)/T$
and let
$G'=\mathrm {N}_G(T)/T$
and let
![]() $V'=V^T$
be the set of fixed points in V under T; then
$V'=V^T$
be the set of fixed points in V under T; then
![]() $V'$
is an étale module for the induced action of
$V'$
is an étale module for the induced action of
![]() $G'$
. Arising from a normaliser of a torus,
$G'$
. Arising from a normaliser of a torus,
![]() $G'$
is a reductive algebraic group. The second construction [Reference Gyoja15, Theorem B] yields a procedure to obtain a super-étale module from an étale module. (This means that the stabiliser of the point in general position is trivial and not just finite.) Given an étale module
$G'$
is a reductive algebraic group. The second construction [Reference Gyoja15, Theorem B] yields a procedure to obtain a super-étale module from an étale module. (This means that the stabiliser of the point in general position is trivial and not just finite.) Given an étale module
![]() $(G,\varrho ,V)$
with
$(G,\varrho ,V)$
with
![]() $v\in V$
in general position and stabiliser
$v\in V$
in general position and stabiliser
![]() $G_v$
, choose
$G_v$
, choose
![]() $1\neq h\in G_v$
and let
$1\neq h\in G_v$
and let
![]() $G''=\mathrm {N}_{G}(h)$
and
$G''=\mathrm {N}_{G}(h)$
and
![]() $V''=V^h$
, the set of fixed points for h in V. Then
$V''=V^h$
, the set of fixed points for h in V. Then
![]() $V''$
is an étale module for the induced action of
$V''$
is an étale module for the induced action of
![]() $G''$
and
$G''$
and
![]() $|G^{\prime \prime }_v|<|G_v|$
. Since
$|G^{\prime \prime }_v|<|G_v|$
. Since
![]() $\langle h\rangle $
is finite,
$\langle h\rangle $
is finite,
![]() $G''$
is also reductive. After finitely many iterations (with
$G''$
is also reductive. After finitely many iterations (with
![]() $G''$
instead of G), one obtains a super-étale module.
$G''$
instead of G), one obtains a super-étale module.
4.1 Relation to carrier algebras
Gyoja’s construction was formulated for groups, but can just as well be formulated for the corresponding Lie algebras. For this let
![]() $\mathfrak {g}$
be a semisimple Lie algebra with nonzero nilpotent
$\mathfrak {g}$
be a semisimple Lie algebra with nonzero nilpotent
![]() $e\in \mathfrak {g}$
, let
$e\in \mathfrak {g}$
, let
![]() $(h,e,f)$
be an
$(h,e,f)$
be an
![]() $\mathfrak {sl}_2$
-triple in
$\mathfrak {sl}_2$
-triple in
![]() $\mathfrak {g}$
and furnish
$\mathfrak {g}$
and furnish
![]() $\mathfrak {g}$
with the
$\mathfrak {g}$
with the
![]() $\mathbb {Z}$
-grading induced by
$\mathbb {Z}$
-grading induced by
![]() $\mathrm {ad}(h_0)$
, where
$\mathrm {ad}(h_0)$
, where
![]() $h_0=\tfrac {1}{2}h$
. Observe now that Gyoja’s method [Reference Gyoja15] replicates the aspect that is of interest to us in Vinberg’s and Bala and Carter’s theory: the focus is on the étale action of the reductive subalgebra of degree
$h_0=\tfrac {1}{2}h$
. Observe now that Gyoja’s method [Reference Gyoja15] replicates the aspect that is of interest to us in Vinberg’s and Bala and Carter’s theory: the focus is on the étale action of the reductive subalgebra of degree
![]() $0$
on the subspace of degree
$0$
on the subspace of degree
![]() $1$
, ignoring the subspaces of higher degree.
$1$
, ignoring the subspaces of higher degree.
Proposition 4.1. Gyoja’s construction, applied to the reductive Lie algebra
![]() $\mathfrak {g}_0$
, the nilpotent element e and the adjoint
$\mathfrak {g}_0$
, the nilpotent element e and the adjoint
![]() $\mathfrak {g}_0$
-module
$\mathfrak {g}_0$
-module
![]() $(\mathrm {ad},\mathfrak {g}_1)$
, produces Vinberg’s étale representation associated with
$(\mathrm {ad},\mathfrak {g}_1)$
, produces Vinberg’s étale representation associated with
![]() $e\in \mathfrak {g}$
.
$e\in \mathfrak {g}$
.
Proof. The stabiliser algebra of e is
![]() $\mathfrak {z}_{\mathfrak {g}_0}(e)$
. We have shown that
$\mathfrak {z}_{\mathfrak {g}_0}(e)$
. We have shown that
![]() $\mathfrak {t}_0=\ker \lambda $
(as introduced in Lemma 3.1) is a maximal toral subalgebra of
$\mathfrak {t}_0=\ker \lambda $
(as introduced in Lemma 3.1) is a maximal toral subalgebra of
![]() $\mathfrak {z}_{\mathfrak {g}_0}(\mathfrak {a})$
, where
$\mathfrak {z}_{\mathfrak {g}_0}(\mathfrak {a})$
, where
![]() $\mathfrak {a}$
is the subalgebra spanned by
$\mathfrak {a}$
is the subalgebra spanned by
![]() $(h,e,f)$
. By [Reference Vinberg24, page 21],
$(h,e,f)$
. By [Reference Vinberg24, page 21],
![]() $\mathfrak {z}_{\mathfrak {g}_0}(\mathfrak {a})=\mathfrak {z}_{\mathfrak {g}_0}(e,h)$
and, since
$\mathfrak {z}_{\mathfrak {g}_0}(\mathfrak {a})=\mathfrak {z}_{\mathfrak {g}_0}(e,h)$
and, since
![]() $h=2h_0\in \mathfrak {g}_0$
, it follows that
$h=2h_0\in \mathfrak {g}_0$
, it follows that
![]() $\mathfrak {z}_{\mathfrak {g}_0}(\mathfrak {a})=\mathfrak {z}_{\mathfrak {g}_0}(e)$
. Thus, a maximal toral subalgebra of
$\mathfrak {z}_{\mathfrak {g}_0}(\mathfrak {a})=\mathfrak {z}_{\mathfrak {g}_0}(e)$
. Thus, a maximal toral subalgebra of
![]() $\mathfrak {z}_{\mathfrak {g}_0}(e)$
is
$\mathfrak {z}_{\mathfrak {g}_0}(e)$
is
![]() $\mathfrak {t}_0=\ker \lambda $
, which takes the place of Gyoja’s
$\mathfrak {t}_0=\ker \lambda $
, which takes the place of Gyoja’s
![]() $\mathfrak {t}$
. Now Lemma 3.1 shows that the fixed point set of
$\mathfrak {t}$
. Now Lemma 3.1 shows that the fixed point set of
![]() $\mathfrak {t}_0$
in
$\mathfrak {t}_0$
in
![]() $\mathfrak {g}_1$
is
$\mathfrak {g}_1$
is
![]() $V'=\mathfrak {z}_{\mathfrak {g}}(\mathfrak {t}_0)\cap \mathfrak {g}_1=\mathfrak {g}(\mathfrak {t},e)_1$
, with
$V'=\mathfrak {z}_{\mathfrak {g}}(\mathfrak {t}_0)\cap \mathfrak {g}_1=\mathfrak {g}(\mathfrak {t},e)_1$
, with
![]() $\mathfrak {t}=\mathbb {C} h\oplus \mathfrak {t}_0$
; moreover,
$\mathfrak {t}=\mathbb {C} h\oplus \mathfrak {t}_0$
; moreover,
![]() $\mathfrak {z}_{\mathfrak {g}_0}(\mathfrak {t}_0)=\mathfrak {g}(\mathfrak {t},e)_0$
is reductive with centre
$\mathfrak {z}_{\mathfrak {g}_0}(\mathfrak {t}_0)=\mathfrak {g}(\mathfrak {t},e)_0$
is reductive with centre
![]() $\mathfrak {t}_0$
. Hence,
$\mathfrak {t}_0$
. Hence,
![]() $\mathfrak {g}'=\mathfrak {z}_{\mathfrak {g}_0}(\mathfrak {t}_0)/\mathfrak {t}_0$
satisfies
$\mathfrak {g}'=\mathfrak {z}_{\mathfrak {g}_0}(\mathfrak {t}_0)/\mathfrak {t}_0$
satisfies
![]() $\mathfrak {g}'\cong [\mathfrak {g}(\mathfrak {t},e)_0,\mathfrak {g}(\mathfrak {t},e)_0]$
, so Gyoja’s
$\mathfrak {g}'\cong [\mathfrak {g}(\mathfrak {t},e)_0,\mathfrak {g}(\mathfrak {t},e)_0]$
, so Gyoja’s
![]() $\mathfrak {g}'$
is the
$\mathfrak {g}'$
is the
![]() $0$
-component of the carrier algebra of e in
$0$
-component of the carrier algebra of e in
![]() $\mathfrak {g}$
. Lastly,
$\mathfrak {g}$
. Lastly,
![]() $V'=\mathfrak {g}(\mathfrak {t},e)_1=[\mathfrak {g}(\mathfrak {t},e),\mathfrak {g}(\mathfrak {t},e)]_1$
is the 1-component of that carrier algebra, since the centre of the reductive
$V'=\mathfrak {g}(\mathfrak {t},e)_1=[\mathfrak {g}(\mathfrak {t},e),\mathfrak {g}(\mathfrak {t},e)]_1$
is the 1-component of that carrier algebra, since the centre of the reductive
![]() $\mathfrak {g}(\mathfrak {t},e)$
is contained in
$\mathfrak {g}(\mathfrak {t},e)$
is contained in
![]() $\mathfrak {g}(\mathfrak {t},e)_0$
.
$\mathfrak {g}(\mathfrak {t},e)_0$
.