Let 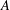$A$ be a subset of 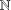$\mathbb{N}$ , the set of all nonnegative integers. For an integer 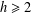$h\geq 2$ , let 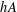$hA$ be the set of all sums of 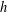$h$ elements of 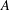$A$ . The set 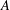$A$ is called an asymptotic basis of order 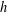$h$ if 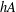$hA$ contains all sufficiently large integers. Otherwise, 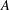$A$ is called an asymptotic nonbasis of order 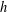$h$ . An asymptotic nonbasis 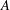$A$ of order 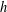$h$ is called a maximal asymptotic nonbasis of order 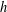$h$ if 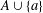$A\cup \{a\}$ is an asymptotic basis of order 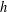$h$ for every 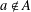$a\notin A$ . In this paper, we construct a sequence of asymptotic nonbases of order 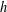$h$ for each 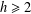$h\geq 2$ , each of which is not a subset of a maximal asymptotic nonbasis of order 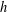$h$ .