Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Saikia, Nipen
2013.
Some New Explicit Values of Quotients of Theta-Function ϕ(q) and Applications to Ramanujan's Continued Fractions.
Journal of Complex Analysis,
Vol. 2013,
Issue. ,
p.
1.
Chaudhary, Mahendra Pal
and
Choi, Junesang
2016.
REPRESENTATIONS OF RAMANUJAN CONTINUED FRACTION IN TERMS OF COMBINATORIAL PARTITION IDENTITIES.
Honam Mathematical Journal,
Vol. 38,
Issue. 2,
p.
367.
Lee, Yoonjin
and
Park, Yoon Kyung
2018.
Three Ramanujan continued fractions with modularity.
Journal of Number Theory,
Vol. 188,
Issue. ,
p.
299.


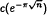 for various positive integers
for various positive integers 