Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-18T16:01:01.439Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonoscillation criteria for Emden-Fowler systems

Published online by Cambridge University Press:  17 April 2009

Lynn H. Erbe  and
Xinzhi Liu
Lynn H. Erbe
Affiliation:
Department of Mathematics, University of Alberta Edmonton, Alberta, Canada T6G 2G1
Xinzhi Liu
Affiliation:
Department of Mathematics, University of Alberta Edmonton, Alberta, Canada T6G 2G1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A number of nonoscillation criteria for the Emden-Fowler system

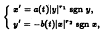
where a(t), b(t) > 0, r1, r2 > 0 and b(t)/a(t) is locally of bounded variation, are established employing energy function techniques. The results obtained here include many known nonoscillation theorems for the classical Emden-Fowler equations as special cases. We illustrate the results obtained with several examples.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 42 , Issue 3 , December 1990 , pp. 455 - 464
Copyright
Copyright © Australian Mathematical Society 1990

References

[1]Atkinson, F.V., ‘On second order nonlinear oscillation’, Pacific J. Math. 5 (1955), 643–647.CrossRefGoogle Scholar
[2]Erbe, L.H., ‘Nonoscillation criteria for second order nonlinear differential equations’, J. Math. Anal. Appl. 108 (1985), 515–527.CrossRefGoogle Scholar
[3]Erbe, L.H., ‘Oscillation and nonoscillation properties for second order nonlinear differential equations’, in Equadiff 82 (Wurzburg, 1982) Lecture Notes in Math., pp. 168–176 (Springer-Verlag, Berlin, Heidelberg, New York, 1983).Google Scholar
[4]Erbe, L.H. and Lu, Hong, ‘Nonoscillation theorems for second order nonlinear differential equations’, Funkcial Ekvac. (to appear).Google Scholar
[5]Erbe, L.H. and Liang, Zhongchao, ‘Continuation and uniqueness for generalized Emden-Fowler systems’, (preprint).Google Scholar
[6]Gollwitzer, H.E., ‘Nonoscillation theorems for nonlinear differential equations’, Proc. Amer. Math. Soc. 26 (1970), 78–84.CrossRefGoogle Scholar
[7]Kwong, M.K. and Wong, J.S.W., ‘Oscillation of Emden-Fowler systems’, Differential Integral Equations 2 (1988), 133–141.Google Scholar
[8]Leighton, W., ‘On self-adjoint differential equations of second order’, J. London Math. Soc. 27 (1952), 37–47.CrossRefGoogle Scholar
[9]Mirzov, D.D., ‘Oscillation of solutions of a system of nonlinear differential equations’, Differenatial'nye Uravneniya 9 (1973), 581–583.Google Scholar
[10]Mirzov, D.D., ‘The oscillation of solutions of a system of nonlinear differential equations’, Mat. Zametki 4 (1974), 571–576.Google Scholar
[11]Mirzov, D.D., ‘Oscillation properties of solutions of a nonlinear Emden-Fowler differential system’, Differenetial'nye Uravneniya 16 (1980), 1980–1984.Google Scholar
[12]Wong, J.S.W., ‘Oscillation theorems for second order nonlinear differential equations’, Bull. Inet. Math. Acad. Sinica 3 (1975), 283–309.Google Scholar
[13]Wong, J.S.W., ‘On the generalized Emden-Fowler equation’, SIAM Rev 17 (1975), 339–360.CrossRefGoogle Scholar