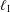Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-04T22:00:06.712Z Has data issue: false hasContentIssue false
  • English
  • Français

NONEXPANSIVE BIJECTIONS TO THE UNIT BALL OF THE $\ell _{1}$ -SUM OF STRICTLY CONVEX BANACH SPACES

Part of: Normed linear spaces and Banach spaces; Banach lattices Nonlinear operators and their properties

Published online by Cambridge University Press:  20 February 2018

V. KADETS Open the ORCID record for V. KADETS [Opens in a new window]  and
O. ZAVARZINA Open the ORCID record for O. ZAVARZINA [Opens in a new window]
V. KADETS
Affiliation:
School of Mathematics and Informatics, V.N. Karazin Kharkiv National University, 61022 Kharkiv, Ukraine email [email protected]
O. ZAVARZINA*
Affiliation:
School of Mathematics and Informatics, V.N. Karazin Kharkiv National University, 61022 Kharkiv, Ukraine email [email protected]
*
✉ [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Extending recent results by Cascales et al. [‘Plasticity of the unit ball of a strictly convex Banach space’, Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. 110(2) (2016), 723–727], we demonstrate that for every Banach space 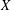$X$ and every collection 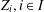$Z_{i},i\in I$ , of strictly convex Banach spaces, every nonexpansive bijection from the unit ball of 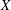$X$ to the unit ball of the sum of 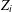$Z_{i}$ by 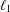$\ell _{1}$ is an isometry.

Keywords

nonexpansive mapunit ballexpand-contract plastic space

MSC classification

Primary: 46B20: Geometry and structure of normed linear spaces
Secondary: 47H09: Contraction-type mappings, nonexpansive mappings, $A$-proper mappings, etc.
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 2 , April 2018 , pp. 285 - 292
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The research of the first author is supported by the Ukrainian Ministry of Science and Education Research Program 0115U000481.

References

Brouwer, L. E. J., ‘Beweis der Invarianz des n-dimensionalen Gebiets’, Math. Ann. 71 (1912), 305–315.CrossRefGoogle Scholar
Cascales, B., Kadets, V., Orihuela, J. and Wingler, E. J., ‘Plasticity of the unit ball of a strictly convex Banach space’, Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A 110(2) (2016), 723–727.CrossRefGoogle Scholar
Kadets, V. and Zavarzina, O., ‘Plasticity of the unit ball of ℓ 1 ’, Visn. Hark. nac. univ. im. V.N. Karazina, Ser.: Mat. prikl. mat. meh. 83 (2017), 4–9.Google Scholar
Mankiewicz, P., ‘On extension of isometries in normed linear spaces’, Bull. Acad. Polon. Sci., Sér. Sci. Math. Astronom. Phys. 20 (1972), 367–371.Google Scholar
Naimpally, S. A., Piotrowski, Z. and Wingler, E. J., ‘Plasticity in metric spaces’, J. Math. Anal. Appl. 313 (2006), 38–48.CrossRefGoogle Scholar
Zavarzina, O., ‘Non-expansive bijections between unit balls of Banach spaces’, Ann. Funct. Anal., to appear, arXiv:1704.06961v2.Google Scholar