Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T01:58:31.624Z Has data issue: false hasContentIssue false
  • English
  • Français

NONEXISTENCE OF A CIRCULANT EXPANDER FAMILY

Part of: Graph theory

Published online by Cambridge University Press:  17 November 2010

KA HIN LEUNG ,
VINH NGUYEN  and
WASIN SO
KA HIN LEUNG
Affiliation:
Department of Mathematics, National Singapore University, Singapore 119260, Republic of Singapore (email: [email protected])
VINH NGUYEN
Affiliation:
Department of Mathematics, San Jose State University, San Jose, CA 95192-0103, USA (email: [email protected])
WASIN SO*
Affiliation:
Department of Mathematics, San Jose State University, San Jose, CA 95192-0103, USA (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The expansion constant of a simple graph G of order n is defined as 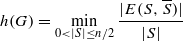where 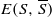denotes the set of edges in G between the vertex subset S and its complement 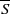. An expander family is a sequence {Gi} of d-regular graphs of increasing order such that h(Gi)>ϵ for some fixed ϵ>0. Existence of such families is known in the literature, but explicit construction is nontrivial. A folklore theorem states that there is no expander family of circulant graphs only. In this note, we provide an elementary proof of this fact by first estimating the second largest eigenvalue of a circulant graph, and then employing Cheeger’s inequalities 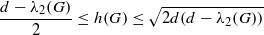where G is a d-regular graph and λ2(G) denotes the second largest eigenvalue of G. Moreover, the associated equality cases are discussed.

Keywords

circulant graphCheeger’s inequalityexpander family

MSC classification

Secondary: 05C50: Graphs and linear algebra (matrices, eigenvalues, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 83 , Issue 1 , February 2011 , pp. 87 - 95
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2010

References

[1]Alon, N. and Roichman, Y., ‘Random Cayley graphs and expanders’, Random Structures Algorithms 5 (1994), 271–284.CrossRefGoogle Scholar
[2]Blum, M., Karp, R. M., Vornberger, O., Papadimitriou, C. H. and Yannakakis, M., ‘The complexity of testing whether a graph is a superconcentrator’, Inform. Process. Lett. 13 (1981), 164–167.CrossRefGoogle Scholar
[3]Cioaba, S., ‘Closed walks and eigenvalues of Abelian Cayley graphs’, C. R. Acad. Sci. Paris, Sér. I 342 (2006), 635–638.CrossRefGoogle Scholar
[4]Friedman, J., Murty, R. and Tillich, J.-P., ‘Spectral estimates for Abelian Cayley graphs’, J. Combin. Theory Ser. B 96 (2006), 111–121.CrossRefGoogle Scholar
[5]Hoory, S., Linial, N. and Wigderson, A., ‘Expander graphs and their applications’, Bull. Amer. Math. Soc. 43 (2006), 439–561.CrossRefGoogle Scholar
[6]Margulis, G. A., ‘Explicit constructions of concentrators’, Probl. Inf. Transm. 9 (1973), 325–332.Google Scholar
[7]Pinsker, M. S., ‘On the complexity of a concentrator’, in: Proceedings, 7th International Teletraffic Conference, Stockholm, 1973, pp. 318/1–318/4.Google Scholar
[8]Titchmarsh, E. C., The Theory of the Riemann Zeta-function (Oxford University Press, Oxford, 1951).Google Scholar