Article contents
Nilpotency and related properties of group extensions
Published online by Cambridge University Press: 17 April 2009
Abstract
Gilbert Baums lag has given sufficient conditions for a group G to be nilpotent in terms of properties of a normal subgroup H and the quotient G/H, and has shown these conditions to be necessary when G is a wreath product and H its base group. His results are extended here to give corresponding conditions for weaker properties ranging from “bounded local nilpotency” to “being an Engel group”. Again we ask whether the sufficient conditions found are necessary when G is non-trivially a wreath product, or is of the form 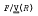 the answer is “yes” for the stronger properties considered, but for the weaker ones the question remains open.
the answer is “yes” for the stronger properties considered, but for the weaker ones the question remains open.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1971
References
- 2
- Cited by


