Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T02:07:05.608Z Has data issue: false hasContentIssue false
  • English
  • Français

NEW REDUCTIONS AND LOGARITHMIC LOWER BOUNDS FOR THE NUMBER OF CONJUGACY CLASSES IN FINITE GROUPS

Part of: Representation theory of groups

Published online by Cambridge University Press:  07 September 2012

EDWARD A. BERTRAM
EDWARD A. BERTRAM*
Affiliation:
Department of Mathematics, University of Hawaii, Honolulu, HI 96822, USA (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The unsolved problem of whether there exists a positive constant $c$ such that the number 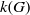$k(G)$ of conjugacy classes in any finite group 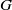$G$ satisfies 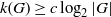$k(G) \geq c \log _{2}|G|$ has attracted attention for many years. Deriving bounds on 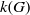$k(G)$ from (that is, reducing the problem to) lower bounds on 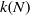$k(N)$ and 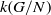$k(G/N)$, 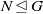$N\trianglelefteq G$, plays a critical role. Recently Keller proved the best lower bound known for solvable groups:

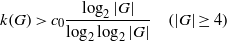\[ k(G)\gt c_{0} \frac {\log _{2}|G|} {\log _{2} \log _{2} |G|}\quad (|G|\geq 4) \]
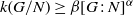using such a reduction. We show that there are many reductions using $k(G/N) \geq \beta [G : N]^{\alpha }$ or 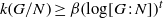$k(G/N) \geq \beta (\log [G : N])^{t}$ which, together with other information about 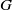$G$ and 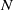$N$ or 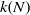$k(N)$, yield a logarithmic lower bound on 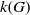$k(G)$.

Keywords

number of conjugacy classessolvable groups

MSC classification

Secondary: 20D60: Arithmetic and combinatorial problems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 87 , Issue 3 , June 2013 , pp. 406 - 424
Copyright
Copyright © 2012 Australian Mathematical Publishing Association Inc. 

References

[Be1]Bertram, E. A., ‘Large centralizers in finite solvable groups’, Israel J. Math. 47 (1984), 335–344.CrossRefGoogle Scholar
[Be2]Bertram, E. A., ‘Lower bounds for the number of conjugacy classes in finite solvable groups’, Israel J. Math. 75 (1991), 243–255.CrossRefGoogle Scholar
[Be3]Bertram, E. A., ‘Lower bounds for the number of conjugacy classes in finite groups’, in: Ischia Group Theory 2004, Contemporary Mathematics, 402 (American Mathematical Society, Providence, RI, 2006), pp. 95–117.CrossRefGoogle Scholar
[Ca]Cartwright, M., ‘The number of conjugacy classes of certain finite groups’, J. Lond. Math. Soc. (2) 36 (1985), 393–404.CrossRefGoogle Scholar
[ET]Erdős, P. & Turán, P., ‘On some problems of a statistical group theory IV’, Acta. Math. Acad. Sci. Hung. 19 (1968), 413–435.CrossRefGoogle Scholar
[HP]Hill, W. M. & Parker, D. B., ‘The nilpotence class of the Frattini subgroup’, Israel J. Math. 15 (1973), 211–215.CrossRefGoogle Scholar
[Hu]Huppert, B., Endliche Gruppen I (Springer, Berlin, 1967).CrossRefGoogle Scholar
[Ke]Keller, T. M., ‘Finite groups have even more conjugacy classes’, Israel J. Math. 181 (2011), 433–444.CrossRefGoogle Scholar
[Ne]Newman, M., ‘A bound for the number of conjugacy classes in a group’, J. Lond. Math. Soc. 43 (1968), 108–110.CrossRefGoogle Scholar
[Ni]Niven, I., ‘Averages of exponents in factoring integers’, Proc. Amer. Math. Soc. 22 (1969), 356–360.CrossRefGoogle Scholar
[Py]Pyber, L., ‘Finite groups have many conjugacy classes’, J. Lond. Math. Soc. (2) 46 (1992), 239–249.CrossRefGoogle Scholar
[Sh]Sherman, G. J., ‘A lower bound for the number of conjugacy classes in a finite nilpotent group’, Pacific J. Math. 80 (1979), 253–254.CrossRefGoogle Scholar
[Ta]Taunt, D. R., ‘On $A$-groups’, Proc. Cambridge Philos. Soc. 45 (1949), 24–42.CrossRefGoogle Scholar
[VS]Vera-López, A. & Sangroniz, J., ‘The finite groups with thirteen and fourteen conjugacy classes’, Math. Nach. 280(5–6) (2007), 676–694.CrossRefGoogle Scholar
[VV1]Vera-López, A. & Vera-López, J., ‘Classification of finite groups according to the number of conjugacy classes’, Israel J. Math. 51 (1985), 305–338.CrossRefGoogle Scholar
[VV2]Vera-López, A. & Vera-López, J., ‘Classification of finite groups according to the number of conjugacy classes II’, Israel J. Math. 56 (1986), 188–221.CrossRefGoogle Scholar