Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-09T13:35:41.131Z Has data issue: false hasContentIssue false
  • English
  • Français

A new definition of variational derivative

Published online by Cambridge University Press:  17 April 2009

Eugene P. Hamilton
Eugene P. Hamilton
Affiliation:
Department of Mathematics, Washington College, Chestertown, Maryland 21620, USA.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

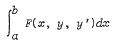It is shown that the functional fails to possess a variational derivative, contrary to what is claimed by Gelfand and Fomin. A modified definition is given with respect to which the functional does possess a variational derivative.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 22 , Issue 2 , October 1980 , pp. 205 - 210
Copyright
Copyright © Australian Mathematical Society 1980

References

[1]Gelfand, I.M., Fomin, S.V., Calculus of variations (translated by Silverman, Richard A.. Prentice-Hall, Englewood Cliffs, New Jersey, 1963).Google Scholar
[2]Voterra, Vito, Theory of functionals and of integral and integro-differential equations (Blackie & Son, London, 1931; reprinted, Dover, New York, 1959).Google Scholar