Published online by Cambridge University Press: 17 April 2009
Let G be a nondiscrete locally compact abelian group with dual group Γ. For 1 ≤ p ≤ ∞, denote by Ap(G) the space of integrable functions on G whose Fourier transforms belong to Lp(Γ). We investigate multipliers from Ap(G) to Aq(G). If G is compact and 2 < p1, p2 < ∞, we show that multipliers of 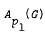 and multipliers of
and multipliers of 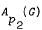 are different, provided Pl ≠ P2. For compact G, we also exhibit a relationship between lr (Γ) and the multipliers from Ap(G) to Aq(G). If G is a compact nonabelian group we observe that the spaces Ap(G) behave in the same way as in the abelian case as far as the multiplier problems are concerned.
are different, provided Pl ≠ P2. For compact G, we also exhibit a relationship between lr (Γ) and the multipliers from Ap(G) to Aq(G). If G is a compact nonabelian group we observe that the spaces Ap(G) behave in the same way as in the abelian case as far as the multiplier problems are concerned.