Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-04-25T14:06:17.440Z Has data issue: false hasContentIssue false
  • English
  • Français

MULTIPLICITY AND ŁOJASIEWICZ EXPONENT OF GENERIC LINEAR SECTIONS OF MONOMIAL IDEALS

Part of: Local rings and semilocal rings Ring extensions and related topics

Published online by Cambridge University Press:  20 February 2015

CARLES BIVIÀ-AUSINA
CARLES BIVIÀ-AUSINA*
Affiliation:
Institut Universitari de Matemàtica Pura i Aplicada, Universitat Politècnica de València, Camí de Vera, s/n, 46022 València, Spain email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We obtain a characterisation of the monomial ideals 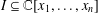$I\subseteq \mathbb{C}[x_{1},\dots ,x_{n}]$ of finite colength that satisfy the condition $e(I)={\mathcal{L}}_{0}^{(1)}(I)\cdots {\mathcal{L}}_{0}^{(n)}(I)$, where 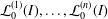${\mathcal{L}}_{0}^{(1)}(I),\dots ,{\mathcal{L}}_{0}^{(n)}(I)$ is the sequence of mixed Łojasiewicz exponents of 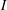$I$ and 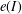$e(I)$ is the Samuel multiplicity of 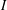$I$. These are the monomial ideals whose integral closure admits a reduction generated by homogeneous polynomials.

Keywords

Łojasiewicz exponentsintegral closure of idealsmixed multiplicities of idealsmonomial idealsNewton polyhedra

MSC classification

Primary: 13B22: Integral closure of rings and ideals ; integrally closed rings, related rings (Japanese, etc.)
Secondary: 13H15: Multiplicity theory and related topics
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 91 , Issue 2 , April 2015 , pp. 191 - 201
Copyright
Copyright © 2015 Australian Mathematical Publishing Association Inc. 

References

Bivià-Ausina, C., ‘Nondegenerate ideals in formal power series rings’, Rocky Mountain J. Math. 34(2) (2004), 495–511.Google Scholar
Bivià-Ausina, C., ‘Jacobian ideals and the Newton non-degeneracy condition’, Proc. Edinb. Math. Soc. (2) 48(1) (2005), 21–36.Google Scholar
Bivià-Ausina, C., ‘Joint reductions of monomial ideals and multiplicity of complex analytic maps’, Math. Res. Lett. 15(2) (2008), 389–407.CrossRefGoogle Scholar
Bivià-Ausina, C., ‘Local Łojasiewicz exponents, Milnor numbers and mixed multiplicities of ideals’, Math. Z. 262(2) (2009), 389–409.Google Scholar
Bivià-Ausina, C. and Encinas, S., ‘Lojasiewicz exponent of families of ideals, Rees mixed multiplicities and Newton filtrations’, Rev. Mat. Complut. 26(2) (2013), 773–798.Google Scholar
Bivià-Ausina, C. and Fukui, T., ‘Mixed Łojasiewicz exponents, log canonical thresholds of ideals and bi-Lipschitz equivalence’, Preprint, 2014, arXiv:1405.2110 [math.AG].Google Scholar
Cox, D., Little, J. and O’Shea, D., Using Algebraic Geometry, 2nd edn, Graduate Texts in Mathematics, 185 (Springer, New York, 2005).Google Scholar
de Fernex, T., Ein, L. and Mustaţă, M., ‘Multiplicities and log canonical threshold’, J. Algebraic Geom. 13(3) (2004), 603–615.Google Scholar
Eisenbud, D., Commutative Algebra with a View Toward Algebraic Geometry, Graduate Texts in Mathematics, 150 (Springer, New York, 2004).Google Scholar
Ewald, G., Combinatorial Convexity and Algebraic Geometry, Graduate Texts in Mathematics, 168 (Springer, New York, 1996).Google Scholar
Herrmann, M., Ikeda, S. and Orbanz, U., Equimultiplicity and Blowing Up. An Algebraic Study. With an Appendix by B. Moonen (Springer, Berlin, 1988).Google Scholar
Hickel, M., ‘Fonction asymptotique de Samuel des sections hyperplanes et multiplicité’, J. Pure Appl. Algebra 214(5) (2010), 634–645.Google Scholar
Howald, J. A., ‘Multiplier ideals of monomial ideals’, Trans. Amer. Math. Soc. 353(7) (2001), 2665–2671.CrossRefGoogle Scholar
Huneke, C. and Swanson, I., Integral Closure of Ideals, Rings, and Modules, London Mathematical Society Lecture Note Series, 336 (Cambridge University Press, Cambridge, 2006).Google Scholar
Lejeune, M. and Teissier, B., ‘Clôture intégrale des idéaux et equisingularité. With an appendix by J. J. Risler’, Ann. Fac. Sci. Toulouse Math. (6) 17(4) (2008), 781–895.CrossRefGoogle Scholar
Li, T. Y. and Wang, X., ‘The BKK root count in ℂn’, Math. Comp. 65(216) (1996), 1477–1484.Google Scholar
Rees, D., ‘Valuations associated with a local ring II’, J. Lond. Math. Soc. 31 (1956), 228–235.Google Scholar
Rees, D., ‘Generalizations of reductions and mixed multiplicities’, J. Lond. Math. Soc. (2) 29 (1984), 397–414.Google Scholar
Rees, D., Lectures on the Asymptotic Theory of Ideals, London Mathematical Society Lecture Note Series, 113 (Cambridge University Press, Cambridge, 1988).Google Scholar
Rojas, M., ‘A convex geometric approach to counting the roots of a polynomial system’, Theoret. Comput. Sci. 133(1) (1994), 105–140.Google Scholar
Rojas, M. and Wang, X., ‘Counting affine roots of polynomial systems via pointed Newton polytopes’, J. Complexity 12(2) (1996), 116–133.CrossRefGoogle Scholar
Teissier, B., ‘Cycles évanescents, sections planes et conditions de Whitney’, Astérisque (7–8) (1973), 285–362.Google Scholar
Teissier, B., ‘Some resonances of Łojasiewicz inequalities’, Wiad. Mat. 48(2) (2012), 271–284.CrossRefGoogle Scholar
Vasconcelos, W., Integral Closure. Rees Algebras, Multiplicities, Algorithms, Springer Monographs in Mathematics (Springer, Berlin, 2005).Google Scholar