No CrossRef data available.
Published online by Cambridge University Press: 25 November 2024
Let  $[a_1(x),a_2(x),\ldots ,a_n(x),\ldots ]$ be the continued fraction expansion of
$[a_1(x),a_2(x),\ldots ,a_n(x),\ldots ]$ be the continued fraction expansion of 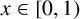 $x\in [0,1)$ and
$x\in [0,1)$ and 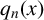 $q_n(x)$ be the denominator of its nth convergent. The irrationality exponent and Khintchine exponent of x are respectively defined by
$q_n(x)$ be the denominator of its nth convergent. The irrationality exponent and Khintchine exponent of x are respectively defined by 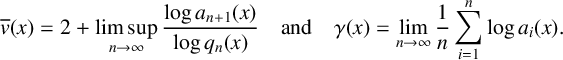 $$ \begin{align*} \overline{v}(x)=2+\limsup_{n\to\infty}\frac{\log a_{n+1}(x)}{\log q_n(x)} \quad \text{and}\quad \gamma(x)=\lim_{n\to\infty}\frac{1}{n}\sum_{i=1}^{n}\log a_i(x). \end{align*} $$
$$ \begin{align*} \overline{v}(x)=2+\limsup_{n\to\infty}\frac{\log a_{n+1}(x)}{\log q_n(x)} \quad \text{and}\quad \gamma(x)=\lim_{n\to\infty}\frac{1}{n}\sum_{i=1}^{n}\log a_i(x). \end{align*} $$
We study the multifractal spectrum of the irrationality exponent and the Khintchine exponent for continued fractions with nondecreasing partial quotients. For any 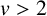 $v>2$, we completely determine the Hausdorff dimensions of the sets
$v>2$, we completely determine the Hausdorff dimensions of the sets 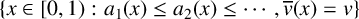 $\{x\in [0,1): a_1(x)\leq a_2(x)\leq \cdots , \overline {v}(x)=v\}$ and
$\{x\in [0,1): a_1(x)\leq a_2(x)\leq \cdots , \overline {v}(x)=v\}$ and 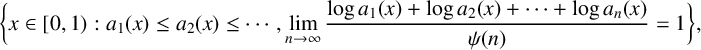 $$ \begin{align*}\bigg\{x\in[0,1): a_1(x)\leq a_2(x)\leq\cdots, \lim\limits_{n\to\infty}\frac{\log a_1(x)+\log a_2(x)+\cdots+\log a_n(x)}{\psi(n)}=1\bigg\},\end{align*} $$
$$ \begin{align*}\bigg\{x\in[0,1): a_1(x)\leq a_2(x)\leq\cdots, \lim\limits_{n\to\infty}\frac{\log a_1(x)+\log a_2(x)+\cdots+\log a_n(x)}{\psi(n)}=1\bigg\},\end{align*} $$
where 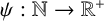 $\psi :\mathbb {N}\rightarrow \mathbb {R}^+$ is a function satisfying
$\psi :\mathbb {N}\rightarrow \mathbb {R}^+$ is a function satisfying 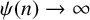 $\psi (n)\to \infty $ as
$\psi (n)\to \infty $ as 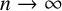 $n\to \infty $.
$n\to \infty $.
Kunkun Song is supported by the National Natural Science Foundation of China (Nos. 12201207, 12371072). Zhenliang Zhang is supported by the Science and Technology Research Program of Chongqing Municipal Education Commission (No. KJQN202100528) and the Natural Science Foundation of Chongqing (No. CSTB2022NSCQ-MSX1255).