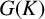1 Introduction
The purpose of this note is to prove a variant of the Mordell–Lang conjecture for semiabelian varieties defined over fields of positive characteristic. More precisely, let G be a semiabelian variety defined over an algebraically closed field K, that is, there exists a short exact sequence of algebraic groups defined over K:
where
![]() $N\ge 0$
is an integer and A is an abelian variety. Assuming K has characteristic
$N\ge 0$
is an integer and A is an abelian variety. Assuming K has characteristic
![]() $p>0$
, then for any subvariety
$p>0$
, then for any subvariety
![]() $X\subseteq G$
defined over K and any finitely generated subgroup
$X\subseteq G$
defined over K and any finitely generated subgroup
![]() $\Gamma \subset G(K)$
, we describe the intersection
$\Gamma \subset G(K)$
, we describe the intersection
![]() $X(K)\cap \Gamma $
. In particular, we fix an error in the paper [Reference Ghioca2] of the first author where a simplified form of such a result was claimed in the case when G is defined over a finite subfield of K; we present several examples showing that the intersection
$X(K)\cap \Gamma $
. In particular, we fix an error in the paper [Reference Ghioca2] of the first author where a simplified form of such a result was claimed in the case when G is defined over a finite subfield of K; we present several examples showing that the intersection
![]() $X(K)\cap \Gamma $
involves the more general F-sets appearing in Definition 1.5.
$X(K)\cap \Gamma $
involves the more general F-sets appearing in Definition 1.5.
1.1 General background
The Mordell–Lang conjecture for semiabelian varieties G defined over fields of characteristic
![]() $0$
predicts that the intersection of a subvariety
$0$
predicts that the intersection of a subvariety
![]() $X\subseteq G$
with a finitely generated subgroup
$X\subseteq G$
with a finitely generated subgroup
![]() $\Gamma $
of G is a finite union of cosets of subgroups of
$\Gamma $
of G is a finite union of cosets of subgroups of
![]() $\Gamma $
. This conjecture was proven by Laurent [Reference Laurent4] in the case of tori, by Faltings [Reference Faltings, Cristante and Messing1] in the case of abelian varieties and by Vojta [Reference Vojta7] in the general case of semiabelian varieties. In particular, their results show that if X is an irreducible subvariety of G which intersects a finitely generated group in a Zariski dense subset, then X must be a translate of a semiabelian subvariety of G.
$\Gamma $
. This conjecture was proven by Laurent [Reference Laurent4] in the case of tori, by Faltings [Reference Faltings, Cristante and Messing1] in the case of abelian varieties and by Vojta [Reference Vojta7] in the general case of semiabelian varieties. In particular, their results show that if X is an irreducible subvariety of G which intersects a finitely generated group in a Zariski dense subset, then X must be a translate of a semiabelian subvariety of G.
The picture for positive characteristic fields K is more complicated due to the existence of the Frobenius endomorphism for varieties defined over finite fields; in particular, it is no longer true that only translates of semiabelian subvarieties of G have the property that they intersect a finitely generated subgroup of G in a Zariski dense subset. Hrushovski [Reference Hrushovski3] obtained the right shape for the irreducible subvarieties X whose intersection with a finitely generated subgroup
![]() $\Gamma $
is Zariski dense.
$\Gamma $
is Zariski dense.
Theorem 1.1 (Hrushovski [Reference Hrushovski3]).
Let G be a semiabelian variety defined over an algebraically closed field K of characteristic p. Let
![]() $\Gamma \subset G(K)$
be a finitely generated subgroup and let
$\Gamma \subset G(K)$
be a finitely generated subgroup and let
![]() $X\subseteq G$
be an irreducible subvariety with the property that
$X\subseteq G$
be an irreducible subvariety with the property that
![]() $X(K)\cap \Gamma $
is Zariski dense in X. Then there exists
$X(K)\cap \Gamma $
is Zariski dense in X. Then there exists
![]() $\gamma \in G(K)$
, a semiabelian subvariety
$\gamma \in G(K)$
, a semiabelian subvariety
![]() $G_0\subseteq G$
defined over K, a semiabelian variety H along with a subvariety
$G_0\subseteq G$
defined over K, a semiabelian variety H along with a subvariety
![]() $X_0\subseteq H$
both defined over a finite subfield
$X_0\subseteq H$
both defined over a finite subfield
![]() $\mathbb F_q$
of K, and a surjective group homomorphism
$\mathbb F_q$
of K, and a surjective group homomorphism
![]() $h:G_0\longrightarrow H$
such that
$h:G_0\longrightarrow H$
such that
![]() $X=\gamma +h^{-1}(X_0)$
.
$X=\gamma +h^{-1}(X_0)$
.
However, [Reference Hrushovski3] left open the description of the actual intersection between the subvariety X and the group
![]() $\Gamma $
. Next, we will address exactly this issue.
$\Gamma $
. Next, we will address exactly this issue.
1.2 The case of semiabelian varieties defined over finite fields and of finitely generated subgroups invariant under the Frobenius endomorphism
Essentially, Hrushovski’s result (see Theorem 1.1) reduced the description of the intersection
![]() $X(K)\cap \Gamma $
to the case when the ambient semiabelian variety is defined over a finite field. Moosa and Scanlon [Reference Moosa and Scanlon5, Reference Moosa and Scanlon6] addressed precisely this problem under an additional assumption on the subgroup
$X(K)\cap \Gamma $
to the case when the ambient semiabelian variety is defined over a finite field. Moosa and Scanlon [Reference Moosa and Scanlon5, Reference Moosa and Scanlon6] addressed precisely this problem under an additional assumption on the subgroup
![]() $\Gamma $
; to state their main result, we introduce some notation.
$\Gamma $
; to state their main result, we introduce some notation.
Definition 1.2. For a semiabelian variety G defined over a finite subfield
![]() $\mathbb F_q$
of an algebraically closed field K of characteristic p, we define a groupless F-set to be any subset of
$\mathbb F_q$
of an algebraically closed field K of characteristic p, we define a groupless F-set to be any subset of
![]() $G(K)$
of the following form:
$G(K)$
of the following form:
 $$ \begin{align} \bigg\{\alpha_0+\sum_{i=1}^r F^{kn_i}(\alpha_i)\colon n_i\in\mathbb{N}\bigg\}, \end{align} $$
$$ \begin{align} \bigg\{\alpha_0+\sum_{i=1}^r F^{kn_i}(\alpha_i)\colon n_i\in\mathbb{N}\bigg\}, \end{align} $$
where
![]() $r\ge 0$
,
$r\ge 0$
,
![]() $\alpha _0,\alpha _1,\ldots , \alpha _r\in G(K)$
and
$\alpha _0,\alpha _1,\ldots , \alpha _r\in G(K)$
and
![]() $k\in \mathbb {N}$
, while F is the Frobenius endomorphism of G corresponding to the finite field
$k\in \mathbb {N}$
, while F is the Frobenius endomorphism of G corresponding to the finite field
![]() $\mathbb F_q$
.
$\mathbb F_q$
.
For any finitely generated subgroup
![]() $\Gamma \subset G(K)$
, we define a groupless F-set in
$\Gamma \subset G(K)$
, we define a groupless F-set in
![]() $\Gamma $
as a groupless F-set contained in
$\Gamma $
as a groupless F-set contained in
![]() $\Gamma $
. Also, an F-set in
$\Gamma $
. Also, an F-set in
![]() $\Gamma $
is any set of the form
$\Gamma $
is any set of the form
![]() $S+B$
, where S is a groupless F-set in
$S+B$
, where S is a groupless F-set in
![]() $\Gamma $
and B is a subgroup of
$\Gamma $
and B is a subgroup of
![]() $\Gamma $
. (For any two subsets B and C of G, as always,
$\Gamma $
. (For any two subsets B and C of G, as always,
![]() $C+B$
is simply the set of all
$C+B$
is simply the set of all
![]() $c+b$
where
$c+b$
where
![]() $b\in B$
and
$b\in B$
and
![]() $c\in C$
.)
$c\in C$
.)
Remark 1.3. In [Reference Moosa and Scanlon6, Theorem B], Moosa and Scanlon allowed for the possibility that a groupless F-set involves sums of F-orbits as in (1.1) of the form
 $$ \begin{align} \alpha_0+\sum_{i=1}^r F^{k_in_i}(\alpha_i)\quad\mbox{(as the}\ n_i\ \mbox{vary in}\ \mathbb{N}\mbox{)}, \end{align} $$
$$ \begin{align} \alpha_0+\sum_{i=1}^r F^{k_in_i}(\alpha_i)\quad\mbox{(as the}\ n_i\ \mbox{vary in}\ \mathbb{N}\mbox{)}, \end{align} $$
for given, but potentially distinct, positive integers
![]() $k_i$
. However, each F-set from (1.2) is a union of finitely many F-sets as in Definition 1.2 (simply by working with k as the least common multiple of
$k_i$
. However, each F-set from (1.2) is a union of finitely many F-sets as in Definition 1.2 (simply by working with k as the least common multiple of
![]() $k_1,\ldots , k_r$
).
$k_1,\ldots , k_r$
).
Theorem 1.4 (Moosa–Scanlon [Reference Moosa and Scanlon6]).
Let G be a semiabelian variety defined over a finite subfield
![]() $\mathbb F_q$
of an algebraically closed field K and let
$\mathbb F_q$
of an algebraically closed field K and let
![]() $F:G\longrightarrow G$
be the Frobenius endomorphism associated to the finite field
$F:G\longrightarrow G$
be the Frobenius endomorphism associated to the finite field
![]() $\mathbb F_q$
. Let
$\mathbb F_q$
. Let
![]() $X\subseteq G$
be a subvariety defined over K and let
$X\subseteq G$
be a subvariety defined over K and let
![]() $\Gamma \subset G(K)$
be a finitely generated subgroup. If
$\Gamma \subset G(K)$
be a finitely generated subgroup. If
![]() $\Gamma $
is invariant under
$\Gamma $
is invariant under
![]() $F^\ell $
for some
$F^\ell $
for some
![]() $\ell \in \mathbb {N}$
, then
$\ell \in \mathbb {N}$
, then
![]() $X(K)\cap \Gamma $
is a finite union of F-sets in
$X(K)\cap \Gamma $
is a finite union of F-sets in
![]() $\Gamma $
.
$\Gamma $
.
1.3 The case of an arbitrary finitely generated subgroup
It is natural to ask whether the description from Theorem 1.4 of the intersection
![]() $X(K)\cap \Gamma $
remains valid when
$X(K)\cap \Gamma $
remains valid when
![]() $\Gamma $
is no longer invariant under a power of the Frobenius endomorphism of G (but we only assume
$\Gamma $
is no longer invariant under a power of the Frobenius endomorphism of G (but we only assume
![]() $\Gamma $
is finitely generated).
$\Gamma $
is finitely generated).
One could consider the
![]() $\mathbb {Z}[F]$
-submodule
$\mathbb {Z}[F]$
-submodule
![]() $\tilde {\Gamma }\subset G(K)$
spanned by
$\tilde {\Gamma }\subset G(K)$
spanned by
![]() $\Gamma $
. Since F is integral over
$\Gamma $
. Since F is integral over
![]() $\mathbb {Z}$
(seen as a subring of
$\mathbb {Z}$
(seen as a subring of
![]() $\mathrm {End}(G)$
), then
$\mathrm {End}(G)$
), then
![]() $\tilde {\Gamma }$
is still finitely generated and so, by Moosa–Scanlon’s result (see Theorem 1.4),
$\tilde {\Gamma }$
is still finitely generated and so, by Moosa–Scanlon’s result (see Theorem 1.4),
![]() $X(K)\cap \tilde {\Gamma }$
is a finite union of F-sets in
$X(K)\cap \tilde {\Gamma }$
is a finite union of F-sets in
![]() $\tilde {\Gamma }$
. So, the problem reduces to understanding the intersection of an F-set S in
$\tilde {\Gamma }$
. So, the problem reduces to understanding the intersection of an F-set S in
![]() $\tilde {\Gamma }$
with
$\tilde {\Gamma }$
with
![]() $\Gamma $
. The first author [Reference Ghioca2, Theorem 3.1] proved that when S is a groupless F-set in
$\Gamma $
. The first author [Reference Ghioca2, Theorem 3.1] proved that when S is a groupless F-set in
![]() $\tilde {\Gamma }$
, then its intersection with
$\tilde {\Gamma }$
, then its intersection with
![]() $\Gamma $
is a finite union of groupless F-sets in
$\Gamma $
is a finite union of groupless F-sets in
![]() $\Gamma $
. Also in [Reference Ghioca2], the first author analysed the intersection with
$\Gamma $
. Also in [Reference Ghioca2], the first author analysed the intersection with
![]() $\Gamma $
of an arbitrary F-set in
$\Gamma $
of an arbitrary F-set in
![]() $\tilde {\Gamma }$
; however, the final assertion from [Reference Ghioca2, Step 3, page 3842] claiming that the general case of an F-set reduces to the groupless case is not valid, as shown by the constructions in Section 2 (see Examples 2.1 and 2.2 which were found by the second author). Essentially, the error from [Reference Ghioca2] was to claim that the pullback of a groupless F-set in
$\tilde {\Gamma }$
; however, the final assertion from [Reference Ghioca2, Step 3, page 3842] claiming that the general case of an F-set reduces to the groupless case is not valid, as shown by the constructions in Section 2 (see Examples 2.1 and 2.2 which were found by the second author). Essentially, the error from [Reference Ghioca2] was to claim that the pullback of a groupless F-set in
![]() $\tilde {\Gamma }$
through a group homomorphism restricted to
$\tilde {\Gamma }$
through a group homomorphism restricted to
![]() $\Gamma $
must be an F-set in
$\Gamma $
must be an F-set in
![]() $\Gamma $
(as in Definition 1.2). Furthermore, Example 2.3 shows that when
$\Gamma $
(as in Definition 1.2). Furthermore, Example 2.3 shows that when
![]() $\Gamma $
is an arbitrary finitely generated subgroup, the intersection
$\Gamma $
is an arbitrary finitely generated subgroup, the intersection
![]() $X(K)\cap \Gamma $
can be quite wild; this motivates our Definition 1.5 which yields the right form of the sets appearing in the intersection of a subvariety of G with a finitely generated group.
$X(K)\cap \Gamma $
can be quite wild; this motivates our Definition 1.5 which yields the right form of the sets appearing in the intersection of a subvariety of G with a finitely generated group.
Definition 1.5. For a semiabelian variety G defined over a finite subfield
![]() $\mathbb F_q$
of an algebraically closed field K of characteristic p and a finitely generated subgroup
$\mathbb F_q$
of an algebraically closed field K of characteristic p and a finitely generated subgroup
![]() ${\Gamma \subset G(K)}$
, we define a generalised F-set in
${\Gamma \subset G(K)}$
, we define a generalised F-set in
![]() $\Gamma $
to be any subset of
$\Gamma $
to be any subset of
![]() $\Gamma $
of the form
$\Gamma $
of the form
where
![]() $\pi :G\longrightarrow H$
is a surjective group homomorphism of semiabelian varieties both defined over a finite subfield of K for which
$\pi :G\longrightarrow H$
is a surjective group homomorphism of semiabelian varieties both defined over a finite subfield of K for which
![]() $\dim (\ker (\pi ))>0$
,
$\dim (\ker (\pi ))>0$
,
![]() $\pi |_\Gamma $
is its restriction to the subgroup
$\pi |_\Gamma $
is its restriction to the subgroup
![]() $\Gamma $
and
$\Gamma $
and
![]() $S\subset H(K)$
is a groupless F-set in
$S\subset H(K)$
is a groupless F-set in
![]() $\pi (\Gamma )$
.
$\pi (\Gamma )$
.
Note that H may be defined over another finite subfield
![]() ${\mathbb F}_{q'}\subset K$
and thus the set S from (1.3) is a groupless F-set in
${\mathbb F}_{q'}\subset K$
and thus the set S from (1.3) is a groupless F-set in
![]() $\pi (\Gamma )$
where F stands for the Frobenius endomorphism of H associated to the finite field
$\pi (\Gamma )$
where F stands for the Frobenius endomorphism of H associated to the finite field
![]() ${\mathbb F}_{q'}$
.
${\mathbb F}_{q'}$
.
1.4 Our results
Now we can state our main results, first for describing the intersection with a finitely generated group of a subvariety of a semiabelian variety defined over a finite field. We note that even though our results are formulated for semiabelian varieties defined over an algebraically closed field K, one could formulate all of the results working instead with an infinite field K, as observed by the referee.
Theorem 1.6. Let G be a semiabelian variety defined over a finite subfield
![]() $\mathbb F_q$
of an algebraically closed field K of characteristic p. Let
$\mathbb F_q$
of an algebraically closed field K of characteristic p. Let
![]() $X\subset G$
be a subvariety defined over K and let
$X\subset G$
be a subvariety defined over K and let
![]() $\Gamma \subset G(K)$
be a finitely generated subgroup. Then the intersection
$\Gamma \subset G(K)$
be a finitely generated subgroup. Then the intersection
![]() $X(K)\cap \Gamma $
is a union of finitely many groupless F-sets in
$X(K)\cap \Gamma $
is a union of finitely many groupless F-sets in
![]() $\Gamma $
along with finitely many generalised F-sets in
$\Gamma $
along with finitely many generalised F-sets in
![]() $\Gamma $
.
$\Gamma $
.
Our Examples 2.1, 2.2 and 2.3 show that the sets appearing as intersections between a subvariety X of a semiabelian variety G defined over a finite field with a finitely generated subgroup can be quite complicated, well beyond the world of F-sets from Definition 1.2. However, when X is a curve or G is a simple semiabelian variety, then we can show that the intersection
![]() $X(K)\cap \Gamma $
is a finite union of F-sets in
$X(K)\cap \Gamma $
is a finite union of F-sets in
![]() $\Gamma $
.
$\Gamma $
.
Theorem 1.7. Let G be a semiabelian variety defined over a finite subfield of an algebraically closed field K of prime characteristic, let
![]() $X\subseteq G$
be a subvariety defined over K and let
$X\subseteq G$
be a subvariety defined over K and let
![]() $\Gamma \subset G(K)$
be a finitely generated subgroup. If either
$\Gamma \subset G(K)$
be a finitely generated subgroup. If either
![]() $\dim (X)=1$
or G is a simple semiabelian variety (that is, either a simple abelian variety or a
$\dim (X)=1$
or G is a simple semiabelian variety (that is, either a simple abelian variety or a
![]() $1$
-dimensional torus), then
$1$
-dimensional torus), then
![]() $X(K)\cap \Gamma $
is a finite union of F-sets.
$X(K)\cap \Gamma $
is a finite union of F-sets.
Next, combining our Theorem 1.6 with Hrushovski’s result (see Theorem 1.1), we obtain the description of the intersection of a subvariety of an arbitrary semiabelian variety G defined over a field of prime characteristic with a finitely generated subgroup of G. For this end, we introduce the notion of pseudo-generalised F-sets.
Definition 1.8. Let G be a semiabelian variety defined over an algebraically closed field K of characteristic p and let
![]() $\Gamma \subset G(K)$
be a finitely generated subgroup. A pseudo-generalised F-set in
$\Gamma \subset G(K)$
be a finitely generated subgroup. A pseudo-generalised F-set in
![]() $\Gamma $
is a set of the form
$\Gamma $
is a set of the form
where
![]() $x_0\in \Gamma $
,
$x_0\in \Gamma $
,
![]() $G_0\subseteq G$
is a semiabelian subvariety,
$G_0\subseteq G$
is a semiabelian subvariety,
![]() $\Gamma _0=G_0(K)\cap \Gamma $
, H is a semiabelian variety defined over a finite subfield
$\Gamma _0=G_0(K)\cap \Gamma $
, H is a semiabelian variety defined over a finite subfield
![]() ${\mathbb F}_q\subset K$
,
${\mathbb F}_q\subset K$
,
![]() $\pi :G_0\longrightarrow H$
is a surjective group homomorphism of semiabelian varieties and
$\pi :G_0\longrightarrow H$
is a surjective group homomorphism of semiabelian varieties and
![]() $S\subset H(K)$
is a groupless F-set in
$S\subset H(K)$
is a groupless F-set in
![]() $\pi (\Gamma _0)$
.
$\pi (\Gamma _0)$
.
Remark 1.9. In Definition 1.8, if G is defined over a finite subfield of K, then the pseudo-generalised F-sets from Definition 1.8 cover both the groupless F-sets in
![]() $\Gamma $
from Definition 1.2 and also the generalised F-sets in
$\Gamma $
from Definition 1.2 and also the generalised F-sets in
![]() $\Gamma $
from Definition 1.5, but they are a bit more general than those two types of sets.
$\Gamma $
from Definition 1.5, but they are a bit more general than those two types of sets.
Theorem 1.10. Let G be a semiabelian variety defined over an algebraically closed field K of characteristic p, let
![]() $X\subseteq G$
be a subvariety and let
$X\subseteq G$
be a subvariety and let
![]() $\Gamma \subset G(K)$
be a finitely generated group. Then
$\Gamma \subset G(K)$
be a finitely generated group. Then
![]() $X(K)\cap \Gamma $
is a finite union of pseudo-generalised F-sets in
$X(K)\cap \Gamma $
is a finite union of pseudo-generalised F-sets in
![]() $\Gamma $
.
$\Gamma $
.
1.5 Plan for our paper
In Section 2, we introduce three examples which progressively show the complexity of the sets appearing as intersections between a subvariety of a semiabelian variety G with a finitely generated group. Even though in our examples, G is defined over a finite field, each such example can be ‘embedded’ as isotrivial semiabelian subvarieties of a semiabelian variety defined over an arbitrary field of positive characteristic, thus providing complex examples of pseudo-generalised F-sets. In Section 3, we prove Theorems 1.6 and 1.10. Also, we prove Theorem 1.7 as a consequence of two more precise results (see Propositions 3.1 and 3.2) regarding the structure of the intersection
![]() $X(K)\cap \Gamma $
when either X is a curve or G is a simple semiabelian variety.
$X(K)\cap \Gamma $
when either X is a curve or G is a simple semiabelian variety.
2 Examples
Our first example already shows that
![]() $X(K)\cap \Gamma $
is not always an F-set in
$X(K)\cap \Gamma $
is not always an F-set in
![]() $\Gamma $
(when
$\Gamma $
(when
![]() $\Gamma $
is not invariant under a power of the Frobenius endomorphism of G).
$\Gamma $
is not invariant under a power of the Frobenius endomorphism of G).
Example 2.1. We let
![]() $G={\mathbb G}_m^2\times E$
, where E is a supersingular elliptic curve defined over
$G={\mathbb G}_m^2\times E$
, where E is a supersingular elliptic curve defined over
![]() $\mathbb F_p$
; for example, we can take E to be the elliptic curve given by the equation in affine coordinates
$\mathbb F_p$
; for example, we can take E to be the elliptic curve given by the equation in affine coordinates
![]() $y^2=x^3+1$
when
$y^2=x^3+1$
when
![]() $p=5$
, in which case, the square
$p=5$
, in which case, the square
![]() $F^2$
of the usual Frobenius endomorphism of E corresponding to
$F^2$
of the usual Frobenius endomorphism of E corresponding to
![]() $\mathbb {F}_5$
equals the multiplication map
$\mathbb {F}_5$
equals the multiplication map
![]() $[-5]$
on E. We let
$[-5]$
on E. We let
![]() $C\subset {\mathbb G}_m^2$
be the line given by the equation
$C\subset {\mathbb G}_m^2$
be the line given by the equation
![]() $x_2=x_1+1$
and then let
$x_2=x_1+1$
and then let
![]() ${X=C\times E}$
. We let
${X=C\times E}$
. We let
![]() $K=\overline {\mathbb F_p(t)}$
and let
$K=\overline {\mathbb F_p(t)}$
and let
![]() $P\in E(K)$
be a nontorsion point. Finally, we let
$P\in E(K)$
be a nontorsion point. Finally, we let
![]() ${\Gamma \subset G(K)}$
be the cyclic group spanned by
${\Gamma \subset G(K)}$
be the cyclic group spanned by
![]() $Q:=(t,t+1,P)\subset G(K)$
. Then
$Q:=(t,t+1,P)\subset G(K)$
. Then
Furthermore, the set from (2.1) cannot be expressed as a groupless F-set; the closest it comes to being an F-set is expressing it as the following slight twist of groupless F-sets. We let
![]() $Q_1:=(t,t+1,0)\in G(K)$
and
$Q_1:=(t,t+1,0)\in G(K)$
and
![]() $Q_2:=(1,1,P)\in G(K)$
, and then the set from (2.1) is the union of the two sets:
$Q_2:=(1,1,P)\in G(K)$
, and then the set from (2.1) is the union of the two sets:
Now, comparing the sets from (2.2) with the actual (groupless) F-sets, the difference seems quite small and so one might think that perhaps slightly extending the definition of F-sets as in (2.2) would be enough. The main issue in Example 2.1 comes from the fact that the Frobenius endomorphism has ‘different weights’ on the abelian and affine parts of G. It might seem reasonable to think that allowing different weights in the definition of a groupless F-set by considering sets of the form
 $$ \begin{align*}\bigg\{\sum_{i=1}^r\sum_{j=1}^s F^{k_{i,j}\cdot n_j}(\alpha_j)\colon n_j\ge 0\text{ for }j=1,\ldots, s\bigg\}\end{align*} $$
$$ \begin{align*}\bigg\{\sum_{i=1}^r\sum_{j=1}^s F^{k_{i,j}\cdot n_j}(\alpha_j)\colon n_j\ge 0\text{ for }j=1,\ldots, s\bigg\}\end{align*} $$
would suffice for describing
![]() $X(K)\cap \Gamma $
. However, the next example shows that no simple extension of the definition of F-sets would work.
$X(K)\cap \Gamma $
. However, the next example shows that no simple extension of the definition of F-sets would work.
Example 2.2. We still work with
![]() $G={\mathbb G}_m^2\times E$
, but this time, the elliptic curve E is ordinary; for example, we could take
$G={\mathbb G}_m^2\times E$
, but this time, the elliptic curve E is ordinary; for example, we could take
![]() $p=5$
and let E be the elliptic curve given by the equation in affine coordinates
$p=5$
and let E be the elliptic curve given by the equation in affine coordinates
![]() $y^2=x^3+x$
. One can check that the Frobenius endomorphism corresponding to
$y^2=x^3+x$
. One can check that the Frobenius endomorphism corresponding to
![]() ${\mathbb F}_5$
satisfies the integral equation
${\mathbb F}_5$
satisfies the integral equation
![]() $F^2-2F+5=0$
on E. As before, we let
$F^2-2F+5=0$
on E. As before, we let
![]() $K=\overline {\mathbb F_p(t)}$
and we work with the cyclic group
$K=\overline {\mathbb F_p(t)}$
and we work with the cyclic group
![]() $\Gamma $
spanned by
$\Gamma $
spanned by
![]() ${Q:=(t,t+1,P)\in G(K)}$
for some nontorsion point
${Q:=(t,t+1,P)\in G(K)}$
for some nontorsion point
![]() $P\in E(K)$
. Then letting
$P\in E(K)$
. Then letting
![]() $X=C\times E$
, where
$X=C\times E$
, where
![]() $C\subset {\mathbb G}_m^2$
is the line
$C\subset {\mathbb G}_m^2$
is the line
![]() $x_2=x_1+1$
, we find
$x_2=x_1+1$
, we find
However, one can show that the set from (2.3) cannot be split into finitely many sets of the form
 $$ \begin{align} \bigg\{\sum_{i=1}^r\sum_{j=1}^s F^{k_{i,j}n_j}(Q_j)\colon n_j\ge 0\text{ for }j=1,\ldots, s\bigg\}, \end{align} $$
$$ \begin{align} \bigg\{\sum_{i=1}^r\sum_{j=1}^s F^{k_{i,j}n_j}(Q_j)\colon n_j\ge 0\text{ for }j=1,\ldots, s\bigg\}, \end{align} $$
for any given
![]() $r,s\in \mathbb {N}$
and any choice of nonnegative integers
$r,s\in \mathbb {N}$
and any choice of nonnegative integers
![]() $k_{i,j}$
and any choice of given points
$k_{i,j}$
and any choice of given points
![]() $Q_j\in G(K)$
. In other words, even the most complex definition of a groupless F-set as in (2.4) would still not cover a possible intersection
$Q_j\in G(K)$
. In other words, even the most complex definition of a groupless F-set as in (2.4) would still not cover a possible intersection
![]() $X(K)\cap \Gamma $
.
$X(K)\cap \Gamma $
.
Now, Examples 2.1 and 2.2 may still suggest that the intersection
![]() $X(K)\cap \Gamma $
could be expressed using more general (groupless) F-sets in which one would allow also the multiplication-by-p map on G playing a similar role to the Frobenius endomorphism. However, the next example shows that
$X(K)\cap \Gamma $
could be expressed using more general (groupless) F-sets in which one would allow also the multiplication-by-p map on G playing a similar role to the Frobenius endomorphism. However, the next example shows that
![]() $X(K)\cap \Gamma $
may have a very complex structure.
$X(K)\cap \Gamma $
may have a very complex structure.
Example 2.3. We let A and B be semiabelian varieties defined over a finite subfield
![]() $\mathbb F_q$
of an algebraically closed field K, let
$\mathbb F_q$
of an algebraically closed field K, let
![]() $G=A\times B$
and let F be the corresponding Frobenius endomorphism associated to
$G=A\times B$
and let F be the corresponding Frobenius endomorphism associated to
![]() $\mathbb F_q$
. We let h be the minimal (monic) polynomial with integer coefficients for which
$\mathbb F_q$
. We let h be the minimal (monic) polynomial with integer coefficients for which
![]() $h(F)=0$
on B. Depending on the abelian part of the semiabelian variety B, the degree m of the polynomial h may be arbitrarily large.
$h(F)=0$
on B. Depending on the abelian part of the semiabelian variety B, the degree m of the polynomial h may be arbitrarily large.
We let
![]() $C\subset B$
be a curve defined over
$C\subset B$
be a curve defined over
![]() $\mathbb F_q$
with trivial stabiliser in B and let
$\mathbb F_q$
with trivial stabiliser in B and let
![]() ${P\in C(K)}$
be a nontorsion point; one can even choose C and P so that
${P\in C(K)}$
be a nontorsion point; one can even choose C and P so that
![]() $C(K)$
intersects the cyclic
$C(K)$
intersects the cyclic
![]() $\mathbb {Z}[F]$
-module
$\mathbb {Z}[F]$
-module
![]() $\Gamma _1$
spanned by P precisely in the orbit of P under the Frobenius endomorphism F. We also let
$\Gamma _1$
spanned by P precisely in the orbit of P under the Frobenius endomorphism F. We also let
![]() $Q_1,\ldots , Q_m\in A(K)$
be linearly independent points (note that
$Q_1,\ldots , Q_m\in A(K)$
be linearly independent points (note that
![]() $A(K)\otimes _{\mathbb {Z}}\mathbb {Q}$
is an infinite dimensional
$A(K)\otimes _{\mathbb {Z}}\mathbb {Q}$
is an infinite dimensional
![]() $\mathbb {Q}$
-vector space). Then we consider
$\mathbb {Q}$
-vector space). Then we consider
![]() ${X:=A\times C}$
and also consider the group
${X:=A\times C}$
and also consider the group
![]() $\Gamma \subset G(K)$
spanned by the points
$\Gamma \subset G(K)$
spanned by the points
Then letting
![]() $\pi _2:G\longrightarrow B$
be the projection of
$\pi _2:G\longrightarrow B$
be the projection of
![]() $G=A\times B$
on the second coordinate, we have
$G=A\times B$
on the second coordinate, we have
![]() $\pi _2(\Gamma )=\Gamma _1$
because
$\pi _2(\Gamma )=\Gamma _1$
because
![]() $\Gamma _1$
is spanned by the points
$\Gamma _1$
is spanned by the points
since
![]() $\Gamma _1$
is the cyclic
$\Gamma _1$
is the cyclic
![]() $\mathbb {Z}[F]$
-module spanned by P and
$\mathbb {Z}[F]$
-module spanned by P and
![]() $h(F)(P)=0$
. So, we can find m sequences
$h(F)(P)=0$
. So, we can find m sequences
![]() $\{a^{(i)}_{n}\}_{n\ge 0}$
of integers (for
$\{a^{(i)}_{n}\}_{n\ge 0}$
of integers (for
![]() $i=0,\ldots , m-1$
) such that for any
$i=0,\ldots , m-1$
) such that for any
![]() $n\ge 0$
,
$n\ge 0$
,
 $$ \begin{align} F^n(P)=\sum_{i=0}^{m-1}a^{(i)}_n\cdot F^i(P). \end{align} $$
$$ \begin{align} F^n(P)=\sum_{i=0}^{m-1}a^{(i)}_n\cdot F^i(P). \end{align} $$
From (2.5),
![]() $X(K)\cap \Gamma $
is the set
$X(K)\cap \Gamma $
is the set
 $$ \begin{align*} \bigg\{\sum_{i=1}^{m} a^{(i-1)}_n\cdot R_i\colon n\ge 0\bigg\}. \end{align*} $$
$$ \begin{align*} \bigg\{\sum_{i=1}^{m} a^{(i-1)}_n\cdot R_i\colon n\ge 0\bigg\}. \end{align*} $$
So, due to the potential complexity of the coefficients of the polynomial h satisfied by the Frobenius endomorphism (on the semiabelian variety B), the sequences
![]() $\{a^{(i)}_n\}_{n\ge 0}$
may be quite complicated.
$\{a^{(i)}_n\}_{n\ge 0}$
may be quite complicated.
3 Proofs of our main results
Proof of Theorem 1.6.
We proceed by induction on
![]() $\dim (X)$
; the case when
$\dim (X)$
; the case when
![]() $\dim (X)=0$
is obvious since then,
$\dim (X)=0$
is obvious since then,
![]() $X(K)\cap \Gamma $
is a finite set and so each of the groupless F-sets from our intersection are singletons (corresponding to
$X(K)\cap \Gamma $
is a finite set and so each of the groupless F-sets from our intersection are singletons (corresponding to
![]() $r=0$
in (1.1)).
$r=0$
in (1.1)).
Clearly, it suffices to assume X is irreducible. Also, we may assume
![]() $X(K)\cap \Gamma $
is Zariski dense in X since otherwise, we could replace X by the Zariski closure of
$X(K)\cap \Gamma $
is Zariski dense in X since otherwise, we could replace X by the Zariski closure of
![]() ${X(K)\cap \Gamma} $
and use the inductive hypothesis.
${X(K)\cap \Gamma} $
and use the inductive hypothesis.
We let
![]() $U:=\mathrm {Stab}_G(X)$
be the stabiliser of X in G. We have two possibilities depending on whether U is finite or not.
$U:=\mathrm {Stab}_G(X)$
be the stabiliser of X in G. We have two possibilities depending on whether U is finite or not.
Case 1:
![]() $\dim (U)>0$
. In this case, we let
$\dim (U)>0$
. In this case, we let
![]() $\pi _0:G\longrightarrow G/U$
be the natural group homomorphism; in particular,
$\pi _0:G\longrightarrow G/U$
be the natural group homomorphism; in particular,
![]() $G_0:=G/U$
is a semiabelian variety defined over a finite field since U is defined over a finite extension of
$G_0:=G/U$
is a semiabelian variety defined over a finite field since U is defined over a finite extension of
![]() $\mathbb F_q$
. We let
$\mathbb F_q$
. We let
![]() $\Gamma _0:=\pi _0(\Gamma )$
and
$\Gamma _0:=\pi _0(\Gamma )$
and
![]() $X_0:=\pi _0(X)$
.
$X_0:=\pi _0(X)$
.
Since
![]() $\dim (U)>0$
, then
$\dim (U)>0$
, then
![]() $\dim (X_0)<\dim (X)$
and so, by the inductive hypothesis,
$\dim (X_0)<\dim (X)$
and so, by the inductive hypothesis,
![]() $X_0(K)\cap \Gamma _0$
is a union of finitely many groupless F-sets
$X_0(K)\cap \Gamma _0$
is a union of finitely many groupless F-sets
![]() $B_i$
in
$B_i$
in
![]() $\Gamma _0$
along with finitely many generalised F-sets
$\Gamma _0$
along with finitely many generalised F-sets
![]() $C_i$
in
$C_i$
in
![]() $\Gamma _0$
. We have
$\Gamma _0$
. We have
Clearly, each
![]() $(\pi _0|_{\Gamma })^{-1}(B_i)$
is a generalised F-set in
$(\pi _0|_{\Gamma })^{-1}(B_i)$
is a generalised F-set in
![]() $\Gamma $
as in Definition 1.5. Now, each
$\Gamma $
as in Definition 1.5. Now, each
![]() $C_i$
is a set of the form
$C_i$
is a set of the form
where
![]() $f:G_0\longrightarrow H$
is a surjective group homomorphism of semiabelian varieties over K in which
$f:G_0\longrightarrow H$
is a surjective group homomorphism of semiabelian varieties over K in which
![]() $\dim (\ker (f))>0$
and H is defined over a finite extension of
$\dim (\ker (f))>0$
and H is defined over a finite extension of
![]() $\mathbb F_q$
, and
$\mathbb F_q$
, and
![]() $S_0$
is a groupless F-set in
$S_0$
is a groupless F-set in
![]() $f(\Gamma _0)\subset H(K)$
as in Definition 1.2. So, using (3.1), along with the fact that
$f(\Gamma _0)\subset H(K)$
as in Definition 1.2. So, using (3.1), along with the fact that
shows that
![]() $X(K)\cap \Gamma $
has the desired form as in the conclusion of Theorem 1.6.
$X(K)\cap \Gamma $
has the desired form as in the conclusion of Theorem 1.6.
Case 2: U is finite. In this case, we let
![]() $\tilde {\Gamma }$
be the
$\tilde {\Gamma }$
be the
![]() $\mathbb {Z}[F]$
-submodule spanned by
$\mathbb {Z}[F]$
-submodule spanned by
![]() $\Gamma $
inside
$\Gamma $
inside
![]() $G(K)$
; since F is integral over
$G(K)$
; since F is integral over
![]() $\mathbb {Z}$
(inside
$\mathbb {Z}$
(inside
![]() $\mathrm {End}(G)$
), then
$\mathrm {End}(G)$
), then
![]() $\tilde {\Gamma }$
is also a finitely generated subgroup of
$\tilde {\Gamma }$
is also a finitely generated subgroup of
![]() $G(K)$
. According to [Reference Moosa and Scanlon6] (see Theorem 1.4),
$G(K)$
. According to [Reference Moosa and Scanlon6] (see Theorem 1.4),
 $$ \begin{align} X(K)\cap\tilde{\Gamma}=\bigcup_{i=1}^\ell (S_i+\Gamma_i), \end{align} $$
$$ \begin{align} X(K)\cap\tilde{\Gamma}=\bigcup_{i=1}^\ell (S_i+\Gamma_i), \end{align} $$
where each
![]() $S_i\subset \tilde {\Gamma }$
is a groupless F-set as in Definition 1.2, while each
$S_i\subset \tilde {\Gamma }$
is a groupless F-set as in Definition 1.2, while each
![]() $\Gamma _i$
is a subgroup of
$\Gamma _i$
is a subgroup of
![]() $\tilde {\Gamma }$
. Now, since
$\tilde {\Gamma }$
. Now, since
it suffices to prove that for each
![]() $i=1,\ldots , \ell $
, there exists a subset
$i=1,\ldots , \ell $
, there exists a subset
![]() $A_i\subseteq X(K)\cap \Gamma $
which is a union of finitely many groupless F-sets in
$A_i\subseteq X(K)\cap \Gamma $
which is a union of finitely many groupless F-sets in
![]() $\Gamma $
along with finitely many generalised F-sets in
$\Gamma $
along with finitely many generalised F-sets in
![]() $\Gamma $
such that
$\Gamma $
such that
then combining (3.2), (3.3) and (3.4), we see that
 $$ \begin{align*}X(K)\cap\Gamma = \bigcup_{i=1}^\ell (S_i+\Gamma_i)\cap\Gamma = \bigcup_{i=1}^\ell A_i\end{align*} $$
$$ \begin{align*}X(K)\cap\Gamma = \bigcup_{i=1}^\ell (S_i+\Gamma_i)\cap\Gamma = \bigcup_{i=1}^\ell A_i\end{align*} $$
is indeed a finite union of groupless F-sets in
![]() $\Gamma $
along with finitely many generalised F-sets in
$\Gamma $
along with finitely many generalised F-sets in
![]() $\Gamma $
, as claimed in the conclusion of Theorem 1.6.
$\Gamma $
, as claimed in the conclusion of Theorem 1.6.
To prove the existence of a set
![]() $A_i$
(for each
$A_i$
(for each
![]() $i=1,\ldots , \ell $
) as in (3.4), we deal with two additional cases.
$i=1,\ldots , \ell $
) as in (3.4), we deal with two additional cases.
Case 2a:
![]() $\Gamma _i$
is an infinite subgroup. In this case, we let
$\Gamma _i$
is an infinite subgroup. In this case, we let
![]() $X_i$
be the Zariski closure of
$X_i$
be the Zariski closure of
![]() $S_i+\Gamma _i$
; clearly,
$S_i+\Gamma _i$
; clearly,
![]() $X_i\subseteq X$
. We claim that
$X_i\subseteq X$
. We claim that
![]() $X_i$
is a proper closed subvariety of X. Indeed, by construction,
$X_i$
is a proper closed subvariety of X. Indeed, by construction,
![]() $\Gamma _i\subseteq \mathrm {Stab}_G(X_i)$
and since
$\Gamma _i\subseteq \mathrm {Stab}_G(X_i)$
and since
![]() $\Gamma _i$
is infinite, we cannot have
$\Gamma _i$
is infinite, we cannot have
![]() $X_i=X$
because
$X_i=X$
because
![]() $\mathrm {Stab}_G(X)$
is finite. So,
$\mathrm {Stab}_G(X)$
is finite. So,
![]() $\dim (X_i)<\dim (X)$
and by our inductive hypothesis,
$\dim (X_i)<\dim (X)$
and by our inductive hypothesis,
![]() $A_i:=X_i(K)\cap \Gamma $
satisfies the conclusion from Theorem 1.6. Therefore,
$A_i:=X_i(K)\cap \Gamma $
satisfies the conclusion from Theorem 1.6. Therefore,
where
![]() $A_i$
is a union of finitely many groupless F-sets along with finitely many generalised F-sets, as desired for (3.4).
$A_i$
is a union of finitely many groupless F-sets along with finitely many generalised F-sets, as desired for (3.4).
Case 2b:
![]() $\Gamma _i$
is finite. In this case, letting
$\Gamma _i$
is finite. In this case, letting
![]() $s:=\#\Gamma _i$
, we see that
$s:=\#\Gamma _i$
, we see that
![]() $S_i+\Gamma _i$
is a union of s groupless F-sets as in Definition 1.2. Now, [Reference Ghioca2, Theorem 3.1] shows that the intersection of a groupless F-set with a finitely generated group is itself a finite union of groupless F-sets; so,
$S_i+\Gamma _i$
is a union of s groupless F-sets as in Definition 1.2. Now, [Reference Ghioca2, Theorem 3.1] shows that the intersection of a groupless F-set with a finitely generated group is itself a finite union of groupless F-sets; so,
is a finite union of groupless F-sets in
![]() $\Gamma $
as desired for (3.4).
$\Gamma $
as desired for (3.4).
This concludes our proof of Theorem 1.6.
Theorem 1.7 is an immediate corollary of our next two results which provide a more precise form of the intersection between a subvariety X of G with a finitely generated subgroup of
![]() $G(K)$
when X is a curve and when G is a simple semiabelian variety.
$G(K)$
when X is a curve and when G is a simple semiabelian variety.
Proposition 3.1. Let G be a semiabelian variety defined over a finite subfield of an algebraically closed field K, let
![]() $\Gamma \subset G(K)$
be a finitely generated subgroup and let
$\Gamma \subset G(K)$
be a finitely generated subgroup and let
![]() $X\subseteq G$
be an irreducible curve.
$X\subseteq G$
be an irreducible curve.
-
(i) If
 $\dim (\mathrm {Stab}_G(X))>0$
, then
$\dim (\mathrm {Stab}_G(X))>0$
, then
 $X(K)\cap \Gamma $
is a coset of a subgroup of
$X(K)\cap \Gamma $
is a coset of a subgroup of
 $\Gamma $
.
$\Gamma $
. -
(ii) If
 $\mathrm {Stab}_G(X)$
is finite, then
$\mathrm {Stab}_G(X)$
is finite, then
 $X(K)\cap \Gamma $
is a finite union of groupless F-sets.
$X(K)\cap \Gamma $
is a finite union of groupless F-sets.
Proof. The proof of part (i) is immediate since then,
![]() $X=\gamma +G_1$
for some point
$X=\gamma +G_1$
for some point
![]() $\gamma \in G(K)$
and some
$\gamma \in G(K)$
and some
![]() $1$
-dimensional connected algebraic subgroup
$1$
-dimensional connected algebraic subgroup
![]() $G_1\subseteq G$
. So, the intersection
$G_1\subseteq G$
. So, the intersection
![]() $X(K)\cap \Gamma $
is simply a coset of the subgroup
$X(K)\cap \Gamma $
is simply a coset of the subgroup
![]() $G_1(K)\cap \Gamma $
of
$G_1(K)\cap \Gamma $
of
![]() $\Gamma $
.
$\Gamma $
.
Now, we assume
![]() $\mathrm {Stab}_G(X)$
is finite. Then we let
$\mathrm {Stab}_G(X)$
is finite. Then we let
![]() $\tilde {\Gamma }$
be the
$\tilde {\Gamma }$
be the
![]() $\mathbb {Z}[F]$
-submodule of
$\mathbb {Z}[F]$
-submodule of
![]() $G(K)$
spanned by
$G(K)$
spanned by
![]() $\Gamma $
. By Theorem 1.4,
$\Gamma $
. By Theorem 1.4,
![]() $\tilde {\Gamma }$
intersects
$\tilde {\Gamma }$
intersects
![]() $X(K)$
in a finite union of F-sets
$X(K)$
in a finite union of F-sets
![]() $S_i$
in
$S_i$
in
![]() $\tilde {\Gamma }$
. However, then at the expense of replacing each
$\tilde {\Gamma }$
. However, then at the expense of replacing each
![]() $S_i$
with finitely many other F-sets, we may assume that each such F-set is groupless (see also the proof of Case 2b in Theorem 1.6). Finally, by another application of [Reference Ghioca2, Theorem 3.1], each
$S_i$
with finitely many other F-sets, we may assume that each such F-set is groupless (see also the proof of Case 2b in Theorem 1.6). Finally, by another application of [Reference Ghioca2, Theorem 3.1], each
![]() $S_i\cap \Gamma $
is a finite union of groupless F-sets in
$S_i\cap \Gamma $
is a finite union of groupless F-sets in
![]() $\Gamma $
, as desired.
$\Gamma $
, as desired.
Proposition 3.2. Let G be a simple semiabelian variety (that is, either a simple abelian variety or a
![]() $1$
-dimensional torus) defined over a finite subfield of an algebraically closed field K, let
$1$
-dimensional torus) defined over a finite subfield of an algebraically closed field K, let
![]() $\Gamma \subset G(K)$
be a finitely generated group and let
$\Gamma \subset G(K)$
be a finitely generated group and let
![]() $X\subset G$
be a proper closed subvariety. Then,
$X\subset G$
be a proper closed subvariety. Then,
![]() $X(K)\cap \Gamma $
is a finite union of groupless F-sets in
$X(K)\cap \Gamma $
is a finite union of groupless F-sets in
![]() $\Gamma $
.
$\Gamma $
.
Proof. First of all, we note that if
![]() $\Gamma $
is a finite group, then clearly
$\Gamma $
is a finite group, then clearly
![]() $X(K)\cap \Gamma $
is a finite set and thus a finite union of groupless F-sets, as desired.
$X(K)\cap \Gamma $
is a finite set and thus a finite union of groupless F-sets, as desired.
So, from now on, we assume that
![]() $\Gamma $
is infinite. According to Theorem 1.6,
$\Gamma $
is infinite. According to Theorem 1.6,
![]() $X(K)\cap \Gamma $
is a finite union of groupless F-sets in
$X(K)\cap \Gamma $
is a finite union of groupless F-sets in
![]() $\Gamma $
along with (possibly) finitely many generalised F-sets in
$\Gamma $
along with (possibly) finitely many generalised F-sets in
![]() $\Gamma $
. Now, for any such generalised F-set in
$\Gamma $
. Now, for any such generalised F-set in
![]() $\Gamma $
(call it S),
$\Gamma $
(call it S),
where
![]() $\pi :G\longrightarrow H$
is a surjective group homomorphism of semiabelian varieties defined over a finite subfield of K,
$\pi :G\longrightarrow H$
is a surjective group homomorphism of semiabelian varieties defined over a finite subfield of K,
![]() $S_0$
is a groupless F-set in
$S_0$
is a groupless F-set in
![]() $\pi (\Gamma )\subset H(K)$
and moreover,
$\pi (\Gamma )\subset H(K)$
and moreover,
![]() $\dim (\ker (\pi ))>0$
. However, since G is a simple semiabelian variety, this means that
$\dim (\ker (\pi ))>0$
. However, since G is a simple semiabelian variety, this means that
![]() $\ker (\pi )=G$
, that is, H is the trivial group variety and so, S would have to be the entire subgroup
$\ker (\pi )=G$
, that is, H is the trivial group variety and so, S would have to be the entire subgroup
![]() $\Gamma $
. However, then its Zariski closure in G is an infinite algebraic subgroup of G (note that
$\Gamma $
. However, then its Zariski closure in G is an infinite algebraic subgroup of G (note that
![]() $\Gamma $
is assumed now to be infinite) and so, once again because G is simple, we would conclude that
$\Gamma $
is assumed now to be infinite) and so, once again because G is simple, we would conclude that
![]() $\Gamma $
is Zariski dense in G. However, then because
$\Gamma $
is Zariski dense in G. However, then because
![]() $S=\Gamma $
is contained in X, we would have
$S=\Gamma $
is contained in X, we would have
![]() $X=G$
, contradicting the fact that X is a proper closed subvariety of G. Therefore, we have no generalised F-sets in
$X=G$
, contradicting the fact that X is a proper closed subvariety of G. Therefore, we have no generalised F-sets in
![]() $\Gamma $
contained in the intersection
$\Gamma $
contained in the intersection
![]() $X(K)\cap \Gamma $
.
$X(K)\cap \Gamma $
.
This concludes our proof for Proposition 3.2.
Theorem 1.10 follows easily from our Theorem 1.6 combined with Theorem 1.1.
Proof of Theorem 1.10.
Clearly, as argued in the proof of Theorem 1.6, it suffices to prove Theorem 1.10 assuming that X is an irreducible subvariety of G and
![]() $X(K)\cap \Gamma $
is Zariski dense in X. Then Theorem 1.1 yields
$X(K)\cap \Gamma $
is Zariski dense in X. Then Theorem 1.1 yields
where
![]() $\pi :G_0\longrightarrow H$
is a surjective group homomorphism of semiabelian varieties, while
$\pi :G_0\longrightarrow H$
is a surjective group homomorphism of semiabelian varieties, while
![]() $G_0$
is a semiabelian subvariety of G and
$G_0$
is a semiabelian subvariety of G and
![]() $\gamma \in G(K)$
; moreover, H and the subvariety
$\gamma \in G(K)$
; moreover, H and the subvariety
![]() $X_0\subseteq H$
are defined over a finite subfield
$X_0\subseteq H$
are defined over a finite subfield
![]() ${\mathbb F}_q\subset K$
. Then for
${\mathbb F}_q\subset K$
. Then for
![]() $x\in G(K)$
, we have
$x\in G(K)$
, we have
![]() $x\in X(K)$
if and only if ‘
$x\in X(K)$
if and only if ‘
![]() $x-\gamma \in G_0(K)$
and
$x-\gamma \in G_0(K)$
and
![]() $\pi (x-\gamma )\in X_0(K)$
’. We denote
$\pi (x-\gamma )\in X_0(K)$
’. We denote
![]() $\Gamma _0=G_0(K)\cap \Gamma $
.
$\Gamma _0=G_0(K)\cap \Gamma $
.
Pick
![]() $x_0\in X(K)\cap \Gamma $
. Let
$x_0\in X(K)\cap \Gamma $
. Let
![]() $g_0=x_0-\gamma \in G_0(K)$
. We have
$g_0=x_0-\gamma \in G_0(K)$
. We have
![]() $x_0+\Gamma _0=(\gamma +G_0(K))\cap \Gamma $
. As a result, for any
$x_0+\Gamma _0=(\gamma +G_0(K))\cap \Gamma $
. As a result, for any
![]() $x\in \Gamma $
, we have
$x\in \Gamma $
, we have
![]() $x-\gamma \in G_0(K)$
if and only if there exists
$x-\gamma \in G_0(K)$
if and only if there exists
![]() $\gamma _0\in \Gamma _0$
such that
$\gamma _0\in \Gamma _0$
such that
![]() $x=x_0+\gamma _0$
. Thus,
$x=x_0+\gamma _0$
. Thus,
![]() $x-\gamma =g_0+\gamma _0$
and so,
$x-\gamma =g_0+\gamma _0$
and so,
![]() $\pi (x-\gamma )\in X_0(K)$
yields
$\pi (x-\gamma )\in X_0(K)$
yields
![]() $\pi (\gamma _0)\in -\pi (g_0)+X_0(K)$
.
$\pi (\gamma _0)\in -\pi (g_0)+X_0(K)$
.
Let
![]() $X_0'=-\pi (g_0)+X_0$
which is a subvariety of H. The discussion above implies that
$X_0'=-\pi (g_0)+X_0$
which is a subvariety of H. The discussion above implies that
![]() $X(K)\cap \Gamma =x_0+(\pi |_{\Gamma _0})^{-1}(X_0'(K)\cap \pi (\Gamma _0))$
. So, considering the subvariety
$X(K)\cap \Gamma =x_0+(\pi |_{\Gamma _0})^{-1}(X_0'(K)\cap \pi (\Gamma _0))$
. So, considering the subvariety
![]() $X_0'\subseteq H$
, along with the finitely generated subgroup
$X_0'\subseteq H$
, along with the finitely generated subgroup
![]() $\pi (\Gamma _0)$
of
$\pi (\Gamma _0)$
of
![]() $H(K)$
, we apply Theorem 1.6 to conclude that the intersection
$H(K)$
, we apply Theorem 1.6 to conclude that the intersection
![]() $X_0'(K)\cap \pi (\Gamma _0)$
is a finite union of generalised F-sets in
$X_0'(K)\cap \pi (\Gamma _0)$
is a finite union of generalised F-sets in
![]() $\pi (\Gamma _0)$
along with finitely many groupless F-sets in
$\pi (\Gamma _0)$
along with finitely many groupless F-sets in
![]() $\pi (\Gamma _0)$
. However, whether S is a generalised F-set in
$\pi (\Gamma _0)$
. However, whether S is a generalised F-set in
![]() $\pi (\Gamma _0)$
or a groupless F-set in
$\pi (\Gamma _0)$
or a groupless F-set in
![]() $\pi (\Gamma _0)$
,
$\pi (\Gamma _0)$
,
![]() $x_0+(\pi |_{\Gamma _0})^{-1}(S)$
will always be a pseudo-generalised F-set in
$x_0+(\pi |_{\Gamma _0})^{-1}(S)$
will always be a pseudo-generalised F-set in
![]() $\Gamma $
(see also Remark 1.9). This shows that
$\Gamma $
(see also Remark 1.9). This shows that
![]() $X(K)\cap \Gamma $
is a finite union of pseudo-generalised F-sets in
$X(K)\cap \Gamma $
is a finite union of pseudo-generalised F-sets in
![]() $\Gamma $
, as desired.
$\Gamma $
, as desired.
Acknowledgements
We thank the anonymous referee for helpful comments and suggestions. The second author is very grateful to his advisor Junyi Xie who introduced this topic to him.