Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-29T00:30:45.940Z Has data issue: false hasContentIssue false
  • English
  • Français

THE MODIFIED QUANTUM WIGNER SYSTEM IN WEIGHTED $L^{2}$ -SPACE

Part of: Elliptic equations and systems Special classes of linear operators Parabolic equations and systems Equations of mathematical physics and other areas of application

Published online by Cambridge University Press:  13 October 2016

BIN LI  and
HAN YANG
BIN LI*
Affiliation:
Department of Mathematics, Jincheng College of Sichuan University, Chengdu 611731, PR China email [email protected]
HAN YANG
Affiliation:
College of Mathematics, Southwest Jiaotong University, Chengdu 611756, PR China email [email protected]
*
✉ [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is concerned with the modified Wigner (respectively, Wigner–Fokker–Planck) Poisson equation. The quantum mechanical model describes the transport of charged particles under the influence of the modified Poisson potential field without (respectively, with) the collision operator. 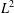Existence and uniqueness of a global mild solution to the initial boundary value problem in one dimension are established on a weighted 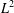$L^{2}$ -space. The main difficulties are to derive a priori estimates on the modified Poisson equation and prove the Lipschitz properties of the appropriate potential term.

Keywords

modified Wigner–Poisson equationmodified Wigner–Poisson–Fokker–Planck equationinitial boundary value problemglobal mild solution

MSC classification

Primary: 35Q40: PDEs in connection with quantum mechanics
Secondary: 35K55: Nonlinear parabolic equations 35J60: Nonlinear elliptic equations 47B44: Accretive operators, dissipative operators, etc.
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 1 , February 2017 , pp. 73 - 83
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Arnold, A., ‘On absorbing boundary conditions for quantum transport equations’, RAIRO–Modélisation Math. Anal. Numérique 28(7) (1994), 853–872.CrossRefGoogle Scholar
Arnold, A., ‘Mathematical properties of quantum evolution equations’, in: Quantum Transport, Lecture Notes in Mathematics, 1946 (eds. Ben Abdallah, N. and Frosali, G.) (Springer, Berlin, 2008), 45–109.CrossRefGoogle Scholar
Arnold, A., Carrillo, J. A. and Dhamo, E., ‘On the periodic Wigner–Poisson–Fokker–Planck system’, J. Math. Anal. Appl. 275 (2002), 263–276.CrossRefGoogle Scholar
Arnold, A., Dhamo, E. and Manzini, C., ‘The Wigner–Poisson–Fokker–Planck system: global-in-time solution and dispersive effects’, Ann. Inst. H. Poincare C: Non Linear Anal. 24(4) (2007), 645–676.CrossRefGoogle Scholar
Arnold, A. and Ringhofer, C., ‘An operator splitting method for the Wigner–Poisson problem’, SIAM J. Numer. Anal. 33(4) (1996), 1622–1643.CrossRefGoogle Scholar
Benmlih, K. and Kavian, O., ‘Existence and asymptotic behaviour of standing waves for quasilinear Schrödinger–Poisson systems in R 3 ’, Ann. Inst. H. Poincare C: Non Linear Anal. 25(3) (2008), 449–470.Google Scholar
Brezzi, F. and Markowich, P. A., ‘The three-dimensional Wigner–Poisson problem: existence, uniqueness and approximation’, Math. Methods Appl. Sci. 14(1) (1991), 35–61.CrossRefGoogle Scholar
Cañizo, J. A., López, J. L. and Nieto, J., ‘‘Global L 1 theory and regularity for the 3D nonlinear Wigner–Poisson–Fokker–Planck system’, J. Differential Equations 198 (2004), 356–373.CrossRefGoogle Scholar
Degond, P. and Markowich, P. A., ‘A mathematical analysis of quantum transport in three-dimensional crystals’, Ann. Mat. Pura Appl. (4) 160(1) (1991), 171–191.CrossRefGoogle Scholar
Han, Y., The Initial-Boundary Value Problem to a Class of the Regularization for the Vlasov Equation with Non-Newtonian Potential, PhD Thesis, Jilin University, 2009 (in Chinese).Google Scholar
Illner, R., ‘Existence, uniqueness and asymptotic behavior of Wigner–Poisson and Vlasov–Poisson systems: a survey’, Transport Theory Statist. Phys. 26(1–2) (1997), 195–207.Google Scholar
Ling, L., The Initial-Boundary Value Problem to a Class of the Regularization for the Nonlinear Vlasov Equation with Non-Newtonian Potential, PhD Thesis, Jilin University, 2011 (in Chinese).Google Scholar
Manzini, C., ‘The three dimensional Wigner–Poisson problem with inflow boundary conditions’, J. Math. Anal. Appl. 313(1) (2006), 184–196.CrossRefGoogle Scholar
Manzini, C. and Barletti, L., ‘An analysis of the Wigner–Poisson problem with time dependent, inflow boundary conditions’, Nonlinear Anal. Theory Methods Appl. 60(1) (2005), 77–100.CrossRefGoogle Scholar
Markowich, P. A., ‘On the equivalence of the Schrödinger and the quantum Liouville equations’, Math. Methods Appl. Sci. 11 (1989), 459–469.CrossRefGoogle Scholar
Markowich, P. A., Ringhofer, C. and Schmeiser, C., Semiconductor Equations (Springer, Wien, 1990).CrossRefGoogle Scholar
Mawhin, J., ‘Leray–Schauder degree: a half century of extensions and applications’, Topol. Methods Nonlinear Anal. 14(2) (1999), 195–228.CrossRefGoogle Scholar
Pazy, A., Semigroups of Linear Operators and Applications to Partial Differential Equations (Springer, Berlin, 1983).CrossRefGoogle Scholar
Simon, J., ‘Compact sets in the space L p (0, T; B)’, Ann. Mat. Pura Appl. (4) 146(1) (1986), 65–96.CrossRefGoogle Scholar
Zweifel, P. F., ‘The Wigner transform and the Wigner–Poisson system’, Transport Theory Statist. Phys. 22(4) (1993), 459–484.CrossRefGoogle Scholar