Published online by Cambridge University Press: 14 December 2020
Let n be a positive integer and let
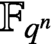 $\mathbb{F} _{q^n}$
be the finite field with
$\mathbb{F} _{q^n}$
be the finite field with
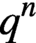 $q^n$
elements, where q is a prime power. We introduce a natural action of the projective semilinear group
$q^n$
elements, where q is a prime power. We introduce a natural action of the projective semilinear group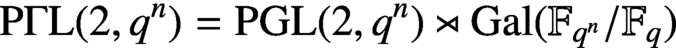 ${\mathrm{P}\Gamma\mathrm{L}} (2, q^n)={\mathrm{PGL}} (2, q^n)\rtimes {\mathrm{Gal}} ({\mathbb F_{q^n}} /\mathbb{F} _q)$
on the set of monic irreducible polynomials over the finite field
${\mathrm{P}\Gamma\mathrm{L}} (2, q^n)={\mathrm{PGL}} (2, q^n)\rtimes {\mathrm{Gal}} ({\mathbb F_{q^n}} /\mathbb{F} _q)$
on the set of monic irreducible polynomials over the finite field
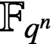 $\mathbb{F} _{q^n}$
. Our main results provide information on the characterisation and number of fixed points.
$\mathbb{F} _{q^n}$
. Our main results provide information on the characterisation and number of fixed points.
The second author was partially supported by FAPEMIG APQ-02973-17, Brazil. The third author was supported by FAPESP 2018/03038-2, Brazil.